Q&A一覧
Q&Aの趣旨
「はて?」「なぜだろう?」と思うことは、科学への第一歩です。
このページでは、科学・理科一般に関すること、および大阪大学理学部・理学研究科に関する質問、学生生活や進路・就職先のことまで、Q&Aコーナーに寄せられた質問のうち一部をご紹介しています。
ふしぎだと思うこと これが科学の芽です
よく観察してたしかめ そして考えること これが科学の茎です
そうして最後になぞがとける これが科学の花です
朝永振一郎(ノーベル物理学賞)
キーワードによる絞り込み検索がおこなえます。
数学について
私は高校2年生ですが、大阪大学理学部数学科を第一志望として下書きを提出したところ、理由が不十分だと指摘されました。
その理由の内容は「数学が好きで、将来就きたいアクチュアリーになるためには数学科で勉強することが必要だと思ったから」です。
これでは大阪大学を志望する理由にならない、大阪大学でなければならない理由がないと学校から言われました。
いろいろと調べましたが、ずばり、志望理由となる大阪大学の魅力を教えていただきたいです。
加えて、アクチュアリーになるために数学科を志望することは最善どうか知りたいです。
アメリカなどで人気No.1 の資格といわれている「アクチュアリー」は簡単に言えば、保険商品の不確実性の分析や評価を行う専門家です。
資格取得に必要な5科目合格までには、平均7、8年かかってしまうほどの難関資格です。
「アクチュアリー」になるためには、確率・統計をベースに生命保険、損害保険、年金数理などを学ぶ必要があります。
普通の数学と応用数学の両方勉強しないといけないことが資格の合格難度を高めています。
ですからアクチュアリーになるには数学科に進学することがとても有利だと思います。
大阪大学理学部数学科では、ほとんどの科目が「普通の数学」の科目で、アクチュアリー関係では唯一つ「保険数学」があるだけです。
アクチュアリー志望であっても、学部の四年間は通常の学生と同じように数学の力を養成して頂くことになります。
大学院に進学すれば、実務関係のある講師による授業も含め、アクチュアリー関係の科目が8個(2021年度)あって充実しています。つまり、大阪大学でアクチュアリー教育を受けようとするならば、まずは、学部でしっかり普通の数学の力をつけてから、大学院に進学して実務に関することを勉強して下さい、ということです。
そういうわけで、アクチュアリー志望であれば数学科に進学するのは良い選択であると思われます。
最後に大阪大学を志望する理由についてですが、そもそもあなたがなぜ大阪大学を仮の志望校としたのかも分からないわけで、なんともこちらからは判断しにくいことです。進路指導の先生ともう一度相談してください。
大学およびその周辺の雰囲気を知りたいということであれば、一度見学に来るという手もあります。例えば学園祭などの大学のイベントであるとかオープンキャンパスなどもあります。
こういった行事の詳細についてはウェブページなどですぐに情報を得ることができます。
私は数学科の卒業生なのですが現在アルバイトで塾講師をやっております。
そこで中学生から次のような質問をされました。
「10/3=3.3333…なのに3.3333…×3=9.9999…となるのはなぜか?」
自分は極限の概念で理解しているのでうまく答えられませんでした。
(中学生なので極限はわからないと思いまして)一応、2/4と1/2が(表記が違うが)同じものを表しているように10と9.9999…も同じものを表していると言いましたがあまりいい説明だったとは思いません。
なにか中学生にもわかるようないい説明方法はないでしょうか?
いい案がありましたらお教え下さい。
数を「10/3=3.3333…」のように無限小数で表すというのは、結局のところ無限級数あるいは極限の概念を用いているわけですから、中学生にちゃんとした説明するのは困難だとは思います。
それに、数の実体と数の表記の区別というのはなかなか説明が難しいものです。
このあたりを考慮して、いくつか案を挙げましょう。
「10 と 9.999… が同じものを表している」ということを説明するには、
例えば
「x=9.999... とおくと、
10x=99.999... ですから
10x=99.999... と x=9.999... の両辺をそれぞれ引くと
10x-x=9 。
9x=9 の両辺を9で割って
x=10 。」
という無限小数をうまく消すという方法があります。
また、「10-9.999... を考えてみよう!」
というのも良いかもしれません。
「10-9.9=0.1, 10-9.99=0.01, 10-9.999=0.001,... 」
という計算を見ていけば
10-9.999... =0
がわかり(これは級数の収束の定義に戻って考えているにすぎないのですが)、
10=9.999...
を納得できるかもしれません。
以上が主な案です。それで納得がいかないようであれば、「3.3333…」というような無限小数による表記がいったいどのような意味であるかということを逆に聞いてみたりして無限を取り扱うのは難しいということをわかってもらい、それは高校以降でするのだということを伝えるなり、それに関する何らかの本を紹介するなりするしかないように思います。
僕は高校2年生で将来中学校の数学の教師になろうと考えています。
教員養成学部以外での免許の取得が難しくなったそうですが、理学部の数学科からでは教師になるのは大変になるのでしょうか?
いろいろ進路の事で真面目に悩んでいるのでよろしくお願いします。
大阪大学理学部数学科では、卒業時に中学校教諭一種免許状(数学)や高等学校教諭一種免許状(数学)を取得することができます。ただし、数学科に配当されている一般教養科目・専門教育科目の他に、「教育の基礎的理解に関する科目等」と呼ばれる科目を、理学部数学科の卒業要件単位とは別に27単位修得する必要があります。この中に中学校や高校で実施する「教育実習」も含まれます(学部4年次に実施)。また、中学校教諭一種免許状を取得する際は、社会福祉施設や特別支援学校での「介護等の体験」が必要になります(主に学部3年次に実施)。
大阪大学理学部数学科の少なくとも1/3位の学生は卒業までに教員免許を取得しています。ですから、教員免許を取得することがそれほど大変と言うわけではありません。
また、教員免許を取得するのであれば、大阪大学在学中に、中学、高校両方の教員免許を取得することを薦めています。(理学部では多くの学生が頑張って両方取得するようにしています。)
大阪大学数学科では、教員養成大学よりはるかに視野の広いバランスのとれた教育を行っているという自負があります。ティーチングスタッフも研究の最前線で活躍している人がほとんどで充実しています。
数学科を志望している高校2年の学生です。
高校の数学授業内容とは全く関係ありませんが、個人的に EulerGamma 定数を調べています。
定義式 γ=limn→∞{Σk=1→n{1/k} - log(n)} で表される以外に無限級数を用いた表現方法等、知られていましたら教えてください。
具体的には、私が独自に導出した式
γ=Σn=1→∞{Σk=2→∞{(-1)k*(1/(knk))}}
という式が既に知られているかどうかを教えてください。
ご質問にあった公式は、たとえば http://mathworld.wolfram.com/Euler-MascheroniConstant.html の(14)式にあります。
ちなみに、この「MathWorld」のサイトはオンライン数学辞典として便利なものです。
EulerGamma 定数に収束する級数は数値計算に便利なものがありません。
最近の本には、あまり説明されていないようです。ご質問にあった公式を改良した公式として
Cn= 1+ 1/2 + ... + 1/n - log(n+1/2)
について
γ = Cn -2 Σp:n+1→∞Σk:1→∞1/(2k+1)*1/(2p)2k+1
という公式が数値計算に使われていたようです。この公式を導くヒントを示しておきます:
γ= Cn - (Cn - Cn+1) - (Cn+1 - Cn+2) -...
また、EulerGamma 定数の積分表示式が、「数学公式III」(岩波全書)13ページにいくつか紹介されています。
被積分函数を適当に級数展開することにより、さまざまな形の級数表示を得ることができるでしょう。
ガンマ函数の入門書として、現在発売されている本:
・「ガンマ関数入門」(日本評論社)
・E.アルティン/著、上野健爾/訳・解説
数値解析に詳しい本(入手困難と思います):
・「ガンマ函数の理論と応用」柴垣和三雄, 岩波書店(1952)
古典物理学に,剛体の回転を表現するオイラーの方程式があります。
この解は、剛体ボディ固定座標系の角速度の関数として、ヤコビの楕円関数を用いて表現されます。
自分で恒等変換で解いてみると(正確には後述の文献の解法を辿ると)、
(角速度の微分)^2=(角速度)^2の関数 (1)
という途中過程に辿り付きます。
勿論、参考文献のように(1)の両辺の平方根を取り
(角速度の微分)=+(角速度)の関数 (2)
とすれば、ヤコビの楕円関数として解けます。しかし、(2)では符号の+を既知としなくてはならず、また符号切り替えは一般には恒等変換にならないと思います。そしてこの疑問は以下へ続きます。
(2)の解のヤコビの楕円関数のうち、母数が1の場合はオイラーの方程式の特異解であり、separatrix(セパラトリクス)と呼ばれています。
一般解が周期解であるのに対してseparatrixは収束解です。
物理現象で言うと、一般解はニューテーション運動なのに対し、separatrixはシングルスピンです。
しかし一般解もそうなのですが、(2)で恒等変換を行っていないので本当のseparatrixは振動解なのではないかと考えています。
これは(1)が何やら円錐曲線めいた微分方程式であること(実際には違うが)も疑問の一因です。
また(これは線形微分方程式のみ?)一般解+特異解がseparatrixの真の解なのではないかというのも疑問の一因です(この場合はやはり振動解?)。
以上自分では難しくて解けないのですが、趣旨としてはseparatrixは振動解なのではないか?ということです。
計算機でオイラーの方程式解の微分方程式を解いて確認しようとしましたが、double精度で行っても解は振動してしまいますがこれが有限語調誤差によるものなのか,理論誤差によるものなのかが判別がつきませんでした。
ちょっと答えにくい質問なので、分かりやすくするために結論を先に書きます。
(a)separatrix の上の点から出発する解は separatrix の終端する不動点に収束する解です。
separatrix の上にのっている解と振動解を繋いで解をつくるようなことは不可能です。
(b)通常の数値計算によって separatrix の解を出そうとすると、振動する解がでて来てしまうのは自然なことです。
これは誤差のある計算をすれば当然そうなります。
(a) について
少し一般の場合で説明します。以下 x は N 次元空間の点と思って下さい。
常微分方程式 x'=f(x) に不変量 E(x) があるときに、関係 E(x)=const を使って変数を減らす操作をするときにはいつでもこのような問題が生じえます。
これはつまり、超曲面 E(x) が複数の成分からなっているためにおこります。
このような場合考える解がどの成分にのっているかを気をつけなくてはなりません。
この点についての巷の解説書の記述は確かに適切とは言えないものが多いのです。適切な解説書を挙げられないのが残念です。
さて平方根の符合の選び方ですが、私が一番論理的単純な納得のしかたと思うのは、このような計算全てを単に解を見つけるための発見法だとみなし、真剣にとらないやり方です。取り敢えず解を探して、その解がどうなっているかは解の一意性定理を使った議論に任せるというやり方です。
これだけではなんなので、質問の方程式の separatrix の上の解についての説明を試みます。
今の場合、状態の空間を
1. 不動点と separatrix たちでなる部分
2. これら以外の部分(振動解によって満たされている)
の二個に分けることができます。それぞれはことなる保存量を持つのでそれぞれの中の点から出発する解は時間が進んで別の部分にうつることはできません。さらに 1. を不動点と separatrix に分けると、これらの間もうつりあうことは出来ません(この部分は常微分方程式の解の一意性を使った議論が必要です。ここをちゃんと書いていない本が多い)。
不動点を取り除いてしまえばseparatrix 同士は連結ではありませんから連続な解は互いにうつりあうことができません。
separatrix の終端近くでは、解は時間とともに終端にある不動点に近付くことしかできません。
従って、ある separatrix の上の点から出発する解を考えるときには別の separatrix を考える必要がないので、その separatrix がのっている方の平方根の符合を選んで変えないことが正当化されます。
周期解の場合はどうしても平方根の符合を両方考える必要があるのでもっと説明が面倒になりますが、考え方は同じです。 (図を描かずに説明するのが難しいのですが例えば上で挙げた戸田の本には図が描いてありますので見て下さい。)
(b)について
平面の上に絵を書いて、方程式を短い時間解いては少し誤差を入れるという操作を繰り返すとどうなるかを想像すれば、なぜ振動してしまうか分かると思います。
これの原因は separatix が終端している不動点が不安定な不動点であるためで、不安定な不動点の近くでは数値計算によってでてきた解の定性的な挙動は信用できません。
僕は高校1年生で、高校の数学にとても魅力を感じ楽しく取り組んでいます。
ですからそれを発展させた数学を学べる数学科に行こうと思っています。
しかし数学というのは既に研究され尽くした学問だと最近感じるようになってきました。
そう考えると意欲がそがれる気分になってしまいます。まだ数学には未開の分野はあるのでしょうか?
今から100年近く前に、ポアンカレが次のような講演をしています。
「かつて数学の未来は不幸であるとの予言があった。
これらの予言者は全ての問題は解けてしまって、未来は落ち穂を拾うことしか許されていない、と言った。
しかし、これらの悲観論者はいつも退却せねばならなかった。
今日は、こういう悲観論者はいないと私は信ずる。」
悲観的な見通しをする人は100年以上前から何人もいて、そのたびに否定されてきています。
100年前の悲観論者が20世紀の数学の発展を見れば、自らの不明を恥じ入るでしょう。
しかし、こうした過去がありながら、数学で、あるいはもっと広く文明において「もうやることはないのではないか」といった問いかけが繰り返されています。
「研究し尽くされたのではないか?」という質問には、直接答えることができません。
この質問の答えは、各人の心の中にあり、各人がどのような知的な努力を行うかにかかっています。
数学の研究において知識の集積は必ずしも重要ではなく、創造的な人間の頭から生れるアイデアが重要になります。
それは過去の未解決問題を解くだけでなく、数学をより単純化しまた新しい研究の方向を照らし出すものです。
これによって、たえず数学の研究には長年蓄積された知識の資産がなくとも若くしてすぐれた成果をあげることが可能なのです。
また、数学の研究においては「知られた問題を解くこと」以上に「新たな問題を見出すこと」のほうが重要な意味を持つことが多いのです。
そして有名な未解決問題が解かれると、そこから新たな問題が生まれ新たな分野の発展を促すことも多いのです。
独創的な精神を人類が失う時代があれば、その時が数学の終わる時でしょう。「人間精神の名誉のために」(ヤコビの言葉)、若者が自由な思考を行う限り、数学の研究が尽きることは決してありません。
そして、数学者ほど知的な活動において完全な自由を持っている人間は少ないのです。
「もうやることはないのではないか?」という悲観論を抱く者に対しては、「あなたは自由な精神を本当の意味で持っているのか」という問いで答えたいと思います。
繰り返しますが、自由な精神が人間の名誉をかけてたゆまず思索する限り、いつまでも数学は前に進んで行くでしょう。
πおよびeを10進展開したとき2つの各数で、奇数と偶数は同じ確率(50%)で現れますか?
問題をもう少し一般化して、「円周率などの定数を十進表示したときに、0~9 がランダムに表れるか」という問題は未解決問題です。
現在のところ
・e や π の小数表示はランダムだと思われている。
・実際に計算機で小数表示をさせると、ほぼランダムに表れる
・ある「正しいと思われる仮定」のもとに π の小数表示はランダムであることが証明された(Bailey-Crandall、2001年)。
仮定自体は証明されていない。
もちろん、十進表示以外の進数表示でも同様で、たとえば二進表示
π=11. 001 001 000 011 111 101...
もランダムであることが、Bailey-Crandall の「仮定」のもとで示されています。
また小数表示の一般論として
・ほとんど全ての実数は、十進表示すると数字がランダムに表れる
・数字がランダムに表れない無理数は知られている
・数字がランダムで表れることが証明された無理数も知られている
ことがわかっています。
整数でない平方根というのは有理数でないことは証明できると思います。
また、現代数学では無理数を有理数の極限として数を定義しているとも聞きました。
これを踏まえて私なりに考えたところ、例えば√2が、実数直線上では、(有理数の極限として定義されている以上)確かな位置として書き表すことは出来ないと思うのです。
しかし、幾何学的には三平方の定理などによって√2の存在や長さが確かにあると簡単に納得することも出来ます。
これに何か矛盾を感じてしまいます。
√2のような整数でない平方根をどのように捉えればよいですか?
(1)ある長さの線分が与えられたときに、定規とコンパスを使ってその sqrt(2) 倍の長さの線分を作図するのは容易です。
従って sqrt(2) という数は「定規とコンパスを使って」定義することが出来ます。
ある数の「確かな位置」というのはどういうことかということを考えてみましょう。
すると、結局のところ問題なのは「何によって」確かなのかということになります。有理数は整数の割算として定義することが出来ます。同じように整数の平方根は例えば定規とコンパスによる作図によって定義できます。
整数の割算を納得している人にとっては有理数の存在は安心して信じることができるでしょう。
同じように初等幾何の作図を当然のことと思っている人には、整数の平方根は確かに存在しています。
しかし例えば四則演算すらも十分に理解していない人は、 10の100 乗のような巨大な数が確かに存在していると信じることはできないのではないでしょうか。
つまり、ある数の実在性はどのような操作を使うことにするのかということに依存します。
整数から出発して四則演算しか使ってはいけないのであれば sqrt(2) は存在しないことになります。
(2)「現代数学では無理数を有理数の極限として数を定義していると...」の部分についてですが、若干誤解しているようです。
sqrt(2) を定義しろと言われれば
「x*x=2 をみたす正の数 x を sqrt(2)と定義する」
と言うのが一番普通でしょう。ここには何も極限は入ってきません。
整数 p,q があるときに、有理数 p/q の定義が
「p=qx をみたす x を p/q と定義する」
であるのと同じようなものです。普通、極限を使って定義するのは、個別の数ではなくて「実数の全体」です。(個別の数で、極限によって定義するものもあります。)
このあたりの実数全体の構成については、微分積分の教科書で数学的に厳密なものの実数論の部分か、あるいはデデキント「数について」岩波文庫を見て下さい。
高等学校で習った数学をみると、まだわかっていないことなどないような気もしますが、いかがでしょうか。
それは数学の論理の高度な完全さがそういう印象を与えるからでしょう。実際にはやらねばならないことが山積しています。自然現象の多くは“非線形な”現象ですが、それらは微分方程式の解を求めて記述されます。厳密な解でなくとも、それを近似する解をコンピュー ターを用いて求めたりします。これなどは数学を工学に応用するにあたってやらねばならぬことでしょう。
大学の数学と高等学校の数学ではずいぶんと違うように聞きましたが本当でしょうか。
ものごとを抽象化する度合いは高まるでしょうが、高等学校の数学から大学の数学に自然に入ってゆけます。高等学校で数学に対して抱いた興味と勉強しようという気持ちをもちつづけて下さい。
高等学校の数学を勉強して数学を面白いと思うようになりました。数学者になりたいという確固たる意思はありませんが、数学科に入学するには動機不十分でしょうか。
数学は自由な学問です。数学を面白いと思う人ならば、まず数学を勉強してみてはどうでしょう。今、あらゆる分野において、数学的要素を身につけた人材が求められています。
数学科における女子学生の比率はどうでしょうか。また女性数学者の活躍はいかがでしょうか。
大阪大学数学科定員47名のうち5~10名が女子学生です。まじめな学習態度で立派な成績を挙げています。世界的にみて女性数学者の数は今世紀に入って増えていますが、日本では欧米に比べてまだまだ少ないと思います。
数学は社会に役立つ学問でしょうか。
もちろんです。1 0進法や2進法のない世界が考えられるでしょうか。数学は有用な公式や理論を他分野の研究者に提供するだけでなく、新しい概念を導入して、物の見方を変えていくこともできるのです。最近の例では、カオス理論やフラクタル次元の理論があります。社会が数学を必要とする度合いはますます大きくなってきています。
数学は紙と鉛筆があればできる学問と聞いていますが、それは本当でしょうか。
多分、それは数学が人間の頭の中でしか生みだし得ないことを例えていったことで、その意味では本当といえます。ただ、実際には、優れた研究者と討論することや文献を読むことなどが、自分のアイデアを育てたり、新しい知識を吸収したりする上で欠かせません。また、考える問題によっては、コンピューターを用いた実験が必要になることもあります。
数学でも実験をするのですか。そういえば、大阪大学数学科には「 実験数学」という講義があると聞きましたが、どのような内容なのですか。
数学の研究は、いくつかの具体的な例について実際に計算を行い、その結果を深く観察することからスタートすることが多いのです。研究のこのような段階を「 実験数学」と名づけました。実験数学の授業内容ですが、低学年の間は、教員の指導の下で、コンピューターなどを用いた様々な数学実験を行います。これにより、他の授業で得た数学の知識が生きた形で身についていきます。こうして高学年になるにつれて徐々に自主的な実験へと進みます。
阪大の数学科が開催している高校生のための公開講座「 現代数学への冒険」 を受講し、とても興味深く 思ったのですが、この講座に関連した参考書はないのですか。
阪大数学科の教員が分担執筆している「 現代数学序説」( 大阪大学出版会)には、現代数学のさまざまな話題が解説されています。この教科書の多くの章は、公開講座での講演原稿をもとにして書かれていますので、高校生にも十分読めると思いますよ。
物理学について
なぜ夜景や星はキラキラ点滅してるように見えるのですか?
光は、屈折率が等しい物質中を進むときはどこまでも直進します。しかし、屈折率が場所によって変化すると、進む方向が曲げられます。
大気の屈折率は圧力や温度や湿度によって変化しますので、もし屈折率が不均一で、しかも時間的に変化すると、光の進む方向も時間的に変化します。
一方、星は非常に遠くにあるので、点光源と見なすことができます。そのため、上空の大気の屈折率が少しゆらぐだけで、目に入る光の強さが変化して、またたいて見えるようになります。これを一般にシンチレーションと言います。
フランス民謡でイギリス人の作品ががもとになって作られた「きらきら星 (Twincle, LittleStar)」はそのことを表現した歌ですね。
なお、変光星といって明るさが実際に変化する星もあります。その原因はいろいろですが、例えばパルサーと呼ばれるものは中性子星が自転しているために明るさが周期的に変化します。
夜景でも街灯の光が私たちの目に届くときに同じような現象が起こります。
それではどうして大気の密度が時間的に変化するのかについて考えてみましょう。
上空に行くと大気の密度が下がってきます。 しかしそれだけは時間的な変化ではありませんので、ゆらぎにはなりません。
一方、温度差や密度差のある大気が触れあうと、上昇気流や下降気流が入り乱れ密度と温度が違う空気のかたまり(気団)ができては消えます。
それらのうちで、星のまたたきに影響が大きいのは上空 11 km 付近にできる10 - 20センチメートル程度の気団です。
密度が高い気団や低い気団が凸レンズや凹レンズのような働きをします。
星のように 非常に小さな点のように見える光は、この気団のゆらぎの影響をより大きく受けますので地上では星からの光が集まって強くなるところと広がって弱くなるところができます。これがきらきら点滅して見える原因です。
一方、金星などの惑星では、像が大きいのでたくさんの点光源の集まりと見なすことができます。
それぞれの点光源のゆらぎが重なり合って平均化されますので、金星全体の明るさの変化はあまり気になりません。
このゆらぎは、気候にもよっても変化します。大気が安定しているときは、ゆらぎが小さくなりますので、またたきは弱くなります。
また地平線に近い角度にある星を見るときは、長い距離の大気を通過しますので真上にある星と比べてまたたきが大きくなります。
同じような現象は夜景を見ているときも起こります。風が吹いたり、ビルなどの熱気による上昇気流が発生すると、空気の密度が時間的に変化して、きらきらして見えます。
ちなみに天文台で鮮明な写真を撮るときには、建物や地表から発生する熱による大気の乱れが影響します。
そのため、天文台は山頂に設置して地表の影響を少なくします。また、寒くてもストーブを使わないようにします。
市街地に近い山では、街灯やネオンサインがじゃまになりますので、人里離れた山の上が良いことになります。
ところで、ハッブル宇宙望遠鏡は高度600キロメートルの真空中にありますので、大気の影響をまったく受けません。
そのため、非常に鮮明な天体写真を撮ることができます。インターネットでその画像が公開されていますのでご覧下さい。
空はなぜ青いんですか? 海はなぜ青いんですか? 緑色の池はなぜそんな色なんですか?
空が青いのと海が青いのとは原因が違います。
その説明の前に、白い光は色々な波長の光が混ざってできていることを思い出して下さい。
カラーテレビの3原色として赤と緑と青がありますが、基本的にはその3種類の色の光の組み合わせを考えてみます。
そのうち、たとえば赤の光がなくなって青と緑の光だけだと青緑色(水色)になります。
あるいは、緑の光がなくなって赤と青だけだとピンク色になります。
青がなくなって赤と緑だけだと黄色になります。波長は青、緑、赤の順番で長くなります。
まず、空が青いのは以下の理由です。
大気中には通常小さな微粒子が浮遊しています。その微粒子によって光が散乱されますが、そのとき波長の短い光がより強く散乱されて向きが変えられます。
したがって太陽からの光のうち、波長の短い青い光が散乱されてそれが私たちの目に入ってきます。
これが空が青い理由です。
一方、赤い光は波長が長いので散乱されにくく遠くまで届きます。
夕日が赤いのは大気中を長い距離にわたって太陽光が進んできたときに青い光は散乱されて徐々に弱くなり、赤い光は散乱されにくく私たちの目に届くからです。
しかし、海(水)の色が青いのは、別の理由です。
実は最近、水の分子が赤い光を吸収することがわかってきました。
コップに入れた水では分かりませんが、数メートルの距離を進むと赤い光が吸収されて弱くなり、次第に水色になってきます。
そのため、きれいな浅い海やプールでは底に届いた光は水色になっています。
その光がもう一度吸収されて私たちの目に届きますので、より水色に見えます。
青や緑の光も少し吸収するので深い海底にはどんな光も届きませんが、数メートルから数十メートルの範囲では太陽からの白色の光は徐々に水色の光になってゆきます。
つまり水の中を進む光は次第に青くなってゆきますが、夕焼けのように赤くなることはありません。
以上の話は、正確に言うと普通の水(H2O)の場合だけです。同じ水でも重水(D2O)の場合は赤い光を吸収しませんので色は付きません。
実際の海や池では、他にも考えなくてはならないことがあります。
ひとつは、プランクトンや汚れです。もしプランクトンが緑色をしていると赤だけでなく青の光も吸収されて弱くなり、残った緑の光が私たちの目に届きますので海は緑色に見えます。
しかし、赤いプランクトンがたくさん繁殖すると赤くなることも起こります。汚れた海に赤潮が発生した状態はそのような場合です。
もうひとつは、海に差し込む光は、太陽からの光だけでなく青空のひかりも届きますので、その散乱光は青になります。
したがって、一般的には水が赤い光を吸収するして青くなる効果と、浮遊しているプランクトンなどが光を吸収する効果と、青空の光が水に入ってくる効果を同時に考えなくてはなりません。
そういう場合は、正確に色の考察をするのは難しいところがあります。
例えば、曇った日の海の色は灰色に近いかも知れませんね。
しかし太陽光がさんさんと降り注ぐ珊瑚礁の海岸の澄んだ海の青さは、最初に説明したように水が赤い光を吸収する効果が最も大きくきいていると思います。
微積分など数学があまり好きではなかったら理学部は向かないですか?
「理学部」といっても、4つの学科(数学科、物理学科、化学科、生物学科)から成っており、それぞれの学科での数学の使われ方や重要性は大きく異なっています。
貴君の希望する物理学科だけに話を絞りましょう。 物理学では理論的研究をするにしても、実験結果の解析をするにしても、数学の知識無しでは非常に困ります。しかし、数学は「研究目的」や「研究対象」ではなく、あくまでも物理学の研究のための「手段」「言語」です。
この点を誤解しないようにしてください。 さらに、物理学で使われる数学にも、非常に多くのものがあります。「微積分」を含む「解析学」は、そのほんの一例にしか過ぎません。「幾何学」も使われますし、「統計学」や「離散数学」も必要になることがあります。
大切なことは、物理学をやるのには「数学が好きかどうか」が問題なのではなく、「物理学が好きかどうか」が本質的に重要です。
極論すれば、物理学が好きならその手段として不可欠な数学がたとえ嫌いだとしても、(嫌いな数学をマスターしながら)研究は進むでしょう。]
僕は今高校3年生で、ただ宇宙が好きで小学校のときに初めて本気になれた勉強が宇宙のことで、宇宙関係の勉強をしたくて大阪大学理学部物理学科志望しました。
大学で実際には地道に微積分などの計算を巧みに利用して物質などを研究してるのですか?
僕は物理は好きですが高校レベルの物理だし、大学に入ったらどうなるかっていうのは見当がつきません。
だから物理をつかう工学部や基礎工学部にも興味があったのでそのオープンキャンパスにもいきました。
理学部独特のおもしろさっていうのはどういったものですか?
大切なのは、地道な勉強や研究を続けていても、「僕はただ宇宙が好きで…、宇宙関係の勉強をしたい」という《初心》や《興味》を、恒に心に抱いておくことです。これが、科学(理科)の発展の原動力になります。
実際の研究では「微積分などの計算を《巧みに》利用」しているわけではありません。
試行錯誤しながら、ある時は「巧みに」、ある時は「失敗」しながら、研究は進みます。
理学部独特のおもしろさは、
●科学的成果がもたらす利益を顧慮する ことなしに、純粋に科学や自然の美しさに惹かれ科学的発見を夢見て勉強・研究を進めることができる。
●一見自明に見える事項に対しても、「なぜ?」という疑問を抱いてその根源を探ろうとする意欲・願望をもっとも直接的に充足できる。
と言えましょう。
自分の興味に従って《徹底的に》理解しようとする努力が、諸手を挙げて奨励されるのは理学部・理学研究科のみだと思います。
僕はこの五年間ほどから宇宙論に強く興味を持っており当然ずっと理学部志望でいました。
しかし、実利がほとんど期待できないこの分野では研究をして生計を立てていけるのは、才能の面でも金銭の面でも限られた一握りの人だけで現実はそれほど甘くはないんだと徐々に気づきました。
それに就職を目指したところで、宇宙論にそれほど潰しが利くとは思えません。
それに矛盾した話かもしれないですが、僕には漠然と、「自分で、企業などにとっての実利となるなんらかの『財』的なモノを生み出したい」、「社会にできるだけ直接的に影響し、社会に必要とされていたい」といった憧れのようなものがあります。この希望は自分の興味のある分野の性質と相対することのように自分でも感じるのです。
「ポスドクまで行ったあげく、30歳で挫折してフリーター完成」のような事態は何としてでも避けたいし、周りの人たちの進めもあって工学部への転向を考えています。
しかし工学部という学部は、特定分野の就職に強い反面、大学に入る時点である程度自分の将来専攻すべき分野を決めておくことが求められると僕は聞いています。
あと一年でそれを決めるには、僕には時間と情報が少なすぎます。
苦しんでおりますが一年以内に最初の決定をしなければなりません。
なるべく将来に選択肢が残るような進路を教えていただけるようお願いします。
真剣に将来のことを考えておられる様子、大変感心致しました。
また色々とやりたいことを持っておられることは、将来それがどのような形でご自分に関わってくるのかによらず宝物です。
大切になさって下さい。
工学部や工学研究科等では企業などで応用に役立つ知識を学ぶことができます。
もし、具体的に希望するものがはっきりしているようでしたら、それを選択するのも良いと思います。
しかし、それで人生が決まると考えるのは、早すぎます。世の中には色々な仕事があります。また一生同じ仕事をしてゆくとは限りません。
ひとつの専門に限定されない広い知識も必要です。そのためには、常に研鑽を積むことを怠らないようにすることが大切です。
一方、理学部や理学研究科では基礎的な学問の研究を行っています。
物理系では、物理現象の基本を理解し解明してゆきます。
実験したり、計算したり、新しい理論を考案したりする中で、それまでわからなかったものが見えてきます。
その成果を世界中に発信します。仮に企業等に就職することを考えた場合でも、それらは十分に生かされます。
実際、大阪大学理学部物理学科およびその上にある大学院(物理学専攻と宇宙地球科学専攻)には沢山の求人が来ます。
卒業生は、工学部や工学研究科出身の人たちと共に活躍しています。
強いて言えば、工学系出身の人はその技術的な可能性を経験の中から突き詰めて技術開発や生産を行うのに対して、理学系出身の人は基本から理解して原理に基づく新しい技術の開発や生産を目指そうとします。実際はその両方が必要です。
また最近の傾向としては、IT関係の求人が増えています。高校教諭になる方もおられます。博士課程(博士後期課程)に進んだ場合でも、修士課程(博士前期課程)や学部生と応募方法に違いはありますが、民間企業に就職する方が増えています。物理学専攻のホームページには、卒業後の進路が掲載されていますのでご覧下さい。
もし研究に強い関心があり、しかもその能力があれば大学等のアカデミックな職につくことは十分可能です。
理学系の研究は必ずしも直接世の中の役に立つことを目指して研究しているわけではありませんが、その研究成果は人類の英知を育む知識の一端を担っています。
宇宙がどうやってできたのか、とか素粒子の根元を解明することは確かに我々の日常生活に直接変化はありません。
しかしそれを知ることによって、人類はより豊かな世界観をもつことができます。
なお、ポスドクという身分は、研究者が独り立ちするための期間と理解して下さい。
研究職に就くと、自分で研究テーマを提案し推進します。ポスドクなどの経験を経ることによって、新しい研究領域を開拓してゆく能力と次の世代を育ててゆく能力が更に身に付きます。
もちろん、物理学には宇宙論に限らず色々な学問があります。興味があったら是非入学を志して下さい。
たとえば、固体結晶が示す性質や機能の探求はそれ自体に尽くせない興味があるだけでなく、その基本原理は応用のための指針としても重要です。
また理学部では物理以外にも様々な基礎学問を研究している研究室があります。宇宙論でなければ工学部という発想はあてはまらないと思います。
ところで、何かひとつの仕事を成し遂げられる能力を持ったひとは他の仕事でもその能力は発揮できるものです。
現時点では、将来の選択肢について情報が十分ではないかも知れませんが、逆に「今、何かを選択したら将来が決まり、安泰」と期待するのも安易な考え方だと思いませんか。
大切なことは何事にも真剣に向かっていることです。
いつかチャンスがやってきたときにそれをものにします。いつも成長していること、それが大切です。
ちなみに「未熟」とは熟す過程にあることを意味します。それには上限はありません。年をとっても上を目指す「未熟者」でいたいものです。
ご健闘を祈ります。
今小5の子の家庭教師をしています。
そこで私が『地球はまん丸じゃなくて、ホントは洋ナシ形なんだよ?』と昔どこかのテレビ番組で言っていたことを教えたら、当たり前ですが『なんでぇ?』ときかれました。
その場でがんばって考えてみたものの、それらしい答えが出ませんでした。なんで、洋ナシ形なんですか?あと本当に洋ナシ形なんですか?
はじめに回答のまとめを書くと、地球は第一近似として球、測地学的には回転楕円体、ジオイド面を誇張して描けば、洋ナシ型ということになりましょう。
1)地球は自然物で様々な凹凸がありますから、完全な球というわけではありません。固体地球科学では、地球の理想的な平均海水面(陸地においても水路を掘ったものとして考える)をジオイド(地球に似たもの)とよびます。これは静かな海水面=等ポテンシャル面であって、局所的な重力の影響により凹凸のある形状になっています。
しかし、ジオイドでは地球の形状を一律に扱えないので、うまくジオイド面をカバーするような回転楕円体を地球の標準形状としています。現在はGRS80とよばれるものが標準楕円体でそれを使った測地の座標系はITRF84と呼ばれます(赤道半径=6378.137, 極半径6356.752 km)(地球楕円体は、天文学で使うIAU楕円体をはじめ数多くあります。ITRF84はGPS(米軍発祥)で使うWGS84との一致もとれています)。
GRS80楕円体の扁平率は(赤道半径-極半径)/赤道半径で表され、1/298.257226 ~0.00335281 となって、極めて球に近い存在です。真の球面とこの楕円体面の高さの差は大きいところでせいぜい10-20km位です。しかし、正確に地球上の位置を指定したい時、真の球面を基準にとってしまうと誤差が大きくなります。航空機の計測位置が数百mずれたら、山に激突するかも知れません。また質量の場合、体積=長さの3乗に従うわけで、重力測定などでは大きな影響が出ます。以上の理由から、測地学では真の球面ではなく楕円体を基準にしています。
2)しかしなぜ、地球は洋ナシ型とも言われるのでしょうか?
それは、標準楕円体面とジオイド面の差を計算してみるとジオイド面の方が北極で約16m高く、北半球中緯度で7mほど低く、南半球中緯度で7mほど高く、南極で約16m-27m低い(数値は大まか)、極端に描けば頭トンガリ出っ尻の形になっているからです(古在さんという有名な学者の業績です)。1)で挙げた真球ー楕円体との差よりもずっと小さい差ですが、これを強調して描けば以下の図のようになります。
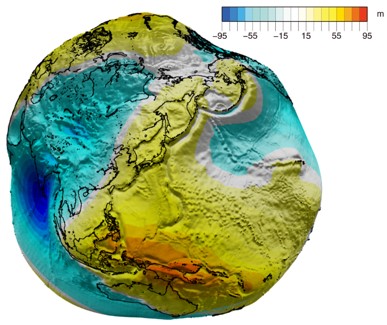
国土地理院WEBより
以下は、複雑な地球の構造の由来に関する補足説明です。
3)地球の形については古代ギリシアの昔から計算されてきました。
赤道半径と極半径のどちらが長いかの論争も大航海時代にありました。
ニュートンは回転流体を考えて、遠心力の働く赤道部分が出っ張るモデルを考えて扁平率=1/230を出しています。しかし地球は前述のように、地球は遠心力だけでは説明できない複雑な形をしています。
4)なぜ、このような変な形をしているのでしょうか? その理由は地球の歴史性に由来すると考えられています。昔、北米大陸などには氷河期に厚い氷の固まりがのっていました。この重みのために大陸は、重油を積んだタンカーのようにマントルに沈降したために変な形をとりました。氷が無くなった今、大陸は少しずつ時間をかけて浮き上がっているところだと考えられています(浮き沈みのつりあいのことをアイソスタシーとよびます)。南半球に関しては海水面が多く、海水は遠心力に短時間に応答してバランスするはずなので、上述の影響はほとんどありません。
球(半径15mm)が空気(常温・1気圧)中を速度v〔m/s〕で運動するときの空気抵抗の近似式を調べています。
v が 0~1 の範囲で良く近似できる式を教えて下さい。(高校2年生)
結論としては、v が 1 m/s ぐらいでは、近似的に速度の二乗に比例して空気抵抗が発生します。
v が 0.1 m/s 以下では、近似的に速度に比例して空気抵抗が発生すると予想されます。
本当は、この問題の答えで一番良いのは自分で工夫して実測する事です。
高校生の物理の知識があれば可能ですし、色々と思わぬ発見もあるはずです。
ただどうしてそうなるのかについては、色々と難しい事も知らなくてはなりません。
たとえば、流体力学です。実際はもっと色々な事がおこりますが、ここでお答えする内容はもっとも単純にまとめたものです。
結論よりもどうしてそうなるのかということに関心を持ってください。
速度 v が 1 m/s ぐらいのときは球の後方に渦が発生して、近似的に速度vの二乗v2に比例して空気抵抗が発生します。
このとき、空気抵抗係数という数値[CD]がよく使われますが、球の表面の形状にも依存します。
球では 0.3 程度の値です。空気抵抗による力は F = -Cv2で与えられます。
ここで、C = [CD]*r*A で、r は空気の密度で1.205kg/m2、Aは断面積で半径 0.015m では 7 x 10-4 m2 です。
なお、空気の密度は自分で測定しても良いのですが、丸善からでている理科年表が役立ちます。
すると、空気抵抗は 2.6 x 10-4 v2 [N] です。
これを測定する方法は、空気抵抗と重力がバランスを取って一定の速度で落下するときの値を測定する方法です。
そこでご質問に近いサイズのピンポン玉の場合を例にとってみますと、半径 19 mm で質量は 2.5 g (最近ルールが変わったかもしれません)ですから、空気抵抗と重力がバランスを取る速さは 7.6 m/s になります。
ちなみに、同じ大きさの球形の氷を落下させると計算上、時速約100 km/s という猛烈な速度になります。
つまり、この大きさのヒョウ(氷の塊)が降って、もし人間を直撃すると大変な事になるのがわかります。
ご質問の速度はこれらの値よりも小さい領域ですので、実験で確かめるためにはピンポン玉ではなく、もっと軽い発泡スチロールでできた球を使う必要があると予想されます。
一方、vが 0.1 m/s 以下では様子が異なります。
空気抵抗は速度に比例し、F = -Bv で与えられます。
速度の二乗に比例する空気抵抗があるときと比較するためには、流体力学で用いるレイノルズ数という概念が役に立ちます。
速度に比例する項と二乗に比例する項を同時に含む形式を考えた場合は、F = -Bv - Cv2 とします。
B の値は知られていませんので、発泡スチロール球の落下速度で実測してみてください。
Is glass, in liquid form, a conductor of electricity?
"Glass" is a term used to specify, in the widest sense, a thermodynamically non-equilibrium state where any disorder is frozen in. The most familiar example of glass is amorphous (or vitreous) solid as often seen as window-glass. The term "glass" is used for this type of glass in the narrowest sense. This type of glass is usually prepared by quenching liquid (resulting in "glassy liquid"), and consequently, has essentially the same structural features. This is why the window glass is often said to be a kind of liquid. Other types of glass also exist. Glassy liquid-crystal is formed by quenching liquid crystals, where orientational order of molecular arrangement exist while translational one does not. Some glassy crystals are formed by quenching orientationally disordered (but positionally ordered) crystals. Spin glass is also glass where disordered spin arrangement is frozen-in, in contrast to previous examples having frozen-in structural disorder.
According to the above interpretation, the term "glass" is not directly correlated with conducting property of matter: Some glasses are conducting whereas others are not. Amorphous metal is electronic conductor. Most amorphous (inorganic) salt will be insulating because ions are effectively immobile in this frozen-in state, though molten salt is surely conducting (electrolyte or ionic conductor). There are however some examples of amorphous salts showing ion conduction. In such cases, small ion(s) run(s) through free volume formed upon glassification (most glass has larger volume than crystalline states). For non-electrolyte and nonmetallic melt, there is no reason to suspect that their quenched glasses are conducting. If your question intended to ask whether is the "melted" glass (in the narrowest sense) conducting, the answer is "no". The glass is mixture of oxides (main component is SiO2), which are insulating.
私は化学科で、環境問題(特に地球温暖化)について学びたいと思っています。
私の学校では、2年進級時に物理・生物の選択を行うのですが、私は生物を選択しました。
けれど大学の授業では物理もカリキュラムに入っているようで、中学までの物理の知識しかない私にはついていくのが難しいでしょうか?(高校2年生)
大学で化学を学ぶには物理の基礎的な知識は必ず必要になります。
それゆえ、高校で物理を履修しておく方が望ましいのは言うまでもありません。
しかし現状では、化学科入学者の1/3程度の学生は生物を選択してきています。
そのため大学の物理の授業について行けず、落ちこぼれる学生がかなり出る問題が生じました。
その対策として、物理未履修者を対象とした授業を最近開講しました。
最終的なゴ ールは同じですので、学習する意欲さえあればきっと大丈夫です。
環境問題に化学からアプローチしたいというあなたの考えは非常に結構だと思います。頑張って下さい。
現在、高校で物理部に所属し、金属線の曲がりに関する独自理論を展開しています。
その理論の根幹となる部分について、どうしても、紙とペンでは解決できない部分があり、質問いたします。
題材は、ごく一般的な金属線です。(ピアノ線と考えていただいて差し支えありません。)
自然な状態が直線状態である金属線を想定します。
そのような金属線を曲げるのには当然エネルギーが必要になりますから、曲がった状態の金属線はエネルギーを持っていると考えることができます。
また、同じ金属線でも、たくさん曲げる方がたくさんエネルギーを要しますから、曲率半径によっても、蓄えられるエネルギーは違ってくるはずです。
ここで、質問します。
円弧の形に曲げられたある特定の金属線において、
蓄えられるエネルギーは曲率半径に対してどのような関係にあるのですか?(曲率半径が十分大きいときにおいて成り立つ近似式でも構いません。)(高校2年生)
ご質問の内容は、材料力学の基本的なことです。
考え方を示しますと、金属線に限らずワイヤーを曲げるとその内側は縮み、外側は伸びまず。
簡単のためにワイヤーの断面が長方形で厚さ2d幅2wの板状とします。これを曲げて円弧にしたとします。
曲げがそれほどきつくないときは弾性変形が可能です。
全体の長さが変化しないと仮定し、曲げた状態で板の中心を通る半径 r の円を考え、円から外側 r + x のところでは x に比例して伸びますので、体積は (r + x)/r 倍になります。
したがって、最も外側では (r + d)/r 倍に増加し、逆に最も内側では (r - d)/r 倍に体積が減少します。
蓄えられた力学的エネルギーは体積変化の二乗に比例します。
円の中心から r + x のところでは、圧縮率(注)を K として、単位体積当たりの力学的エネルギーは
(1/2K)(x/r)2
となります。厚さが 2d で幅が 2w ですから、x について -d から +d まで積分すると、板の単位長さ当たりの力学的エネルギーは
2w(d3)/(3Kr2)
つまり、曲げていないときは r は無限大ですから、力学的エネルギーは蓄えられていません。
曲げると曲率半径の二乗に反比例して、単位長さ当たりの力学的エネルギーは増えてゆきます。
他の係数としては、圧縮率に反比例し厚さの3乗に比例します。幅に比例するのは当然です。これでご質問の答になっているでしょうか?
ここで面白いことに気が付きます。板を 90 度回転して幅と厚さを入れ替えてみます。つまり、2d <=> 2w とすると、
2d(w3)/(3Kr2)
となります。d
断面がHの形をしていて、同じ質量の棒状の材料を使った場合と比較して非常に曲げに強い構造になっていて、ビルの構造材などに広く用いられています。
また、中空のパイプも同様に中空でないものよりも同じ材料で強い構造を作ることが出来ます。
なお、実際には大きく曲げることによって内側が変形して膨らんだり外側がへこんだりすることがあるかもしれません。
また、厚さも多少変化するかもしれません。もし弾性変形を超えて塑性変形を起こす場合は、もとに戻りませんので複雑です。
また、たとえば針金をはじいてピーンと音をたてるような高速変形の場合では断熱変化となり、曲げと共に温度変化も起きるためゆっくり曲げた等温変化のときとは一般に係数が異なります。
より一般的なことは、材料力学と書かれた本をご覧下さい。
(注)圧縮率
体積 V の物体に圧力 dp をかけて dV だけ体積が変化したとき、圧縮率 K は
K dp = -dV/V
で与えられます。K が大きい物質は、同じ圧力を加えたときに変化する体積が大きい(やわらかい)ということです。
一方、体積弾性率Bは圧縮率Kの逆数で与えられます。具体的な数値は、例えば丸善から出ている理科年表を参照して下さい。
弾性材料の歪曲によって蓄えられるエネルギーについて解答をくださり、ありがとうございます。
たいへん参考になります。
話を総合しますと、推論の仮定は
1.弾性材料の中心線の長さは変化しない。
2.蓄えられるエネルギーは体積変化の2乗に比例する。
の2点ですね。
この2点、線状の材料に蓄えられる弾性エネルギーを考察するときの汎用性が非常に高く感じられます。
また、弾性エネルギーが曲率半径の2乗に反比例するということですが、これは、曲率の2乗に比例すると換言できますね。
ところで、付け加えて質問ですが点によって曲率が異なる線状の弾性材料に蓄えられるエネルギーを考察したければ、点におけるエネルギー率(←私の造語です)(次元は[エネルギー/距離])を考えて単純に積分すれば良いのですよね?
また、金属線のねじれによって蓄えられるエネルギーも、仮定1,2を転用して考えればいいのでしょうか?(1の仮定は、「中間半径の面の面積が変化しない」と書き換えるのが妥当な気がしますが・・・、近似度的にはどちらも同程度ですね。)
ご指摘の2点
1. 弾性材料の中心線の長さは変化しない。
2. 蓄えられるエネルギーは体積変化の2乗に比例する。
は仮定と言うよりも近似です。変位が大きいとずれが大きくなります。
1.は直観的にある程度、成り立つと理解できます。
2.は体積変化dVと圧力pにおいて、エネルギー変化が dE=-pdV で与えられることから近似的に導かれます。
そのとき、圧縮率Kについて Kdp=-dV/Vとなることを利用し体積変化の二次の項まで求めると、前回与えた式が得られます。
一般に、変位に比例する力が発生する場合は力学的エネルギーは変位の二乗に比例します。
お考えのように変形した材料の場所ごとのエネルギーが与えられていれば、全体にわたってそれを積分すれば全エネルギーが得られます。
しかし変形した状態をどうやって作るのかについては、別に考えなくてはなりません。
つまり線の形状を与えてから計算するのは比較的簡単ですが、どうやって線を変形させるのかについては結構難しい計算をしなくてはなりません。
これらは私の専門ではありませんので、あまり詳しいことは分かりませんが、線の両端を固定し途中の側面に力を加える場合や、線の片方を固定し他端を引っ張る、曲げるなどの力を加える場合、同様に線の片方を固定して他端をねじる場合があります。
最後のねじる場合は、固体に特徴的な力学です。
具体例としてはスプリングバネです。ねじれ角の二乗に比例してエネルギーが変化しますが、実はフックの法則としてバネ全体の力学としては、高校の教科書で自明なこととして扱われています。
しかし実はその正体は、ねじれの力学だったわけです。
詳しいことについては、是非、材料力学や弾性体力学の本を読まれることをお勧めします。
建築や車両や機械などにおける力学は大変重要な分野だと思います。
さらに時間的変化まで考えると、変位が波として伝わってゆく弾性波の問題に発展します。
現在、力の伝播の実態は何か?について知りたいと考えています。
具体的には、固体を伝播する弾性波、応力波などを想定しています。
一般的に力とは、原子?(分子?)の配置の歪み?が伝播することを弾性波としている?ようです。
しかし私は本当は、力の伝播の第1波は電磁波あるいは電気力のようなものであり、これは非常に高速(光速?)で固体中を伝播し、続いて第2波として第1波の電磁波あるいは電気力による原子の位置歪みが起こり、これが弾性波なのではと考えています。
すなわち位置歪には時定数があるため、電磁波あるいは電気力の後に弾性波が遅れて来るものと考えています。この考え方は正しいですか?
正しい場合には、特に前記の第1波が何なのかと言うことに関して興味がありますので教えて下さい。
また、前記メカニズムを対象とする分野を勉強したいのですが分野を教えて下さい。弾性体学?固体物理学ですか? (技術者)
一般に種類の異なる波が互いに相互作用を持ち、しかも振動数と波長が接近しているときには二つの波が結合した連成波という状態が良い近似になります。
お尋ねの場合は、電磁波と弾性波(固体の分極波)が互いに相互作用を持って伝播する場合で、ポラリトンと呼ばれます。
電磁波はマクスウェルの方程式(古典電磁気学)で明らかなように、電場の時間変化が磁場の発生に磁場の時間変化が電場の発生につながり、それ自身が波として伝わってゆきます。
一方、たとえば電磁波の電場と相互作用するものとして、プラスとマイナスのイオンが互いに逆向きに運動する弾性波が考えられます。
この場合、電磁波の電場によって分極が引き起こされますので、電磁波と分極波の一緒になった連成波として上記のポラリトンと呼ばれる状態が実現します。
一方、弾性波自身も波として空間を伝播する性質があります。
そこで電磁波によるエネルギーの伝播を誘電分散と呼び、それと結合している弾性波自身の伝達を空間分散と呼び、両者を区別して考えます。
一般に電磁波による伝搬速度は速く、弾性波による伝播速度は遅いのが通常ですのでご指摘の応答速度についての説明はおおむね当たっています。
しかし、電磁波と弾性波を別々に考えるのは正しくありません。
つまりポラリトンというひとつの波として伝わります。連成波の状態では、電磁波と弾性波の波長は互いに等しくなっています。エネルギーは互いに接近しています。十分低温で、他の波との散乱が起こらない場合は、このようなポラリトンが最も良い描像です。
しかし温度が高くなると、波の散乱が頻繁に起こり、かならずしも良い描像にはなりません。
上記の場合は、電磁波の振動数と弾性波の振動数が接近している場合に該当しますが、互いに離れているときはポラリトンの概念はそれほど意識する必要はありません。
具体的には弾性波の分極は重い原子核の運動ですので、そのエネルギーは遠赤外線領域で可視光線の光の電場の振動には追随できません。
この場合、可視光線のような振動数に追随できるのは、原子を構成する電子雲の分極(変形)によるものです。
電子は軽いため、電場が作用すると、瞬時に分極します。その効果は、たとえば屈折率が真空の値の1よりも大きいという形で現れます。
もう少し広い見方から言い換えると、電磁波と結合するのは弾性波だけでなく電子雲の分極についても同時に起こるということになります。
これらの詳細については、電磁気学の媒質中の電磁波(マクスウェル方程式)の項をご覧下さい。
また光と物質との相互作用は、光物性の分野が該当しますので、関連する書籍をご一読されることをお勧めします。
たとえば、櫛田孝司著「光物性物理学」朝倉書店、1991年、があります。
さて、弾性波には分極を持つ光学モードと持たない音響モードがあります。
電磁波と結合するのは光学モードです。似たような組み合わせは、電磁波と励起子(電子系の励起状態の一種)が結合した励起子ポラリトン、プラズモンと光学フォノンが結合した状態、電子の波とフォノンが結合したポーラロンなど多種多様です。
これらは固体物理学の根幹をなす概念です。固体中だけで存在できるフォノンなどは素励起(準粒子)と呼ばれ、それらを他の粒子と組み合わせた連成波も新しい素励起として重要な役割を担っています。
原子間に力を及ぼす相互作用としては電場(磁性体では磁場も可能)を介したものがありますが、これは長距離力です。
もう一つは電子の波動関数が関係するものです。そのひとつとして、隣接する原子の波動関数が互いにパウリの排他律によって退けあうことによる斥力があります。
最も端的な例は、希ガス原子間の斥力です(非常に弱い引力もありますが)。
希ガス原子の電子配置では占有されている電子軌道が完全に詰まっていて、それらの原子が互いに接近すると電子は互いの軌道に入ることができません。
もしこのようなパウリの排他律による斥力がなければ、我々は地上に立っていられないことでしょう。
また化学結合による力もあります。共有結合はその代表的な例で、原子間の距離と結合角が決まりそれからはずれると復元力が働きます。
これらは固体物理学や物性化学の本をご覧になると詳しく述べられています。
光を粒子として考えることで電磁波の運動量が与えられる事は解るのですが、それでは弾性波の運動量はどのように与えられるのでしょうか?
弾性波のミクロなメカニズムが格子振動?であり、格子振動を量子化したフォノン?を考慮することにより、電子の運動量と同じようにフォノン?の運動量を与えることと等価なのでしょうか?
また弾性波の屈折は、光波の屈折と同じ法則で起こるとして考えて良いのでしょうか?
考えてよいとすると、光波での屈折率と弾性波の屈折率とは異なるのでしょうか?
またレーザートラップ技術では光波を屈折した場合には運動量保存則により、光波の運動量変化分の逆符号が屈折因子(例えばレンズ)に印加されますが、弾性波の場合にも運動量保存が成立して、弾性波の運動量変化分の逆符号が媒質に印加されるのでしょうか? (技術者)
答を先に述べますと、結晶中の運動量は結晶運動量と呼ばれ、素粒子が持つ運動量とは異なります。
結晶中では、擬似的に運動量が保存しますが、素粒子の運動量の保存則とは原理が違います。
一方、素粒子としての運動量は全系で見ると保存しますので孤立原子ではその効果が無視できない場合があり、それがレーザートラップ技術などに利用されます。
少し長くなりますが、以下に説明します。
結晶は並進対称性がありますので、結晶中を伝播する波は相互作用がなければ長い距離を進み続けます。
そのため波長が明確にきまり、その逆数に2πをかけた波数ベクトルが定義できます。
プランクの定数を2πで割ったもの(/h)に波数ベクトルをかけたものが波の運動量です(つまり、プランクの定数を波長で割ったものが運動量になります)。
結晶では波が別の波と相互作用して向きやエネルギーを変えるとき、その前後では全系のエネルギーが保存するだけでなく逆格子ベクトルに相当する不定項を含む形で運動量の保存則も成立します。
これは素粒子における運動量保存則と一見似ていますが、原理は異なります。
もっとも簡単な逆格子ベクトルは、格子定数の逆数に2πをかけたもので定義されたくさんの組み合わせがあります。
j番目の逆格子ベクトルをGjとして、波数ベクトル保存則(/hを掛ければ運動量についての式になる)を式で書くと、以下のようになります。
まず、波1と波2の波数ベクトルをそれぞれk1、k2とし、それが互いに相互作用した後に、k1'とk2'に変化(散乱)したとします。
その際、
k1 + k2 = k1' + k2' + Gj
となります。
Gjは0の場合も可能ですが、0でないときこれをウンクラップUmklapp過程と呼びます。
波であれば、弾性波(フォノン)でも電子の波でも結晶中での状況は同じです。
一方、アモルファス固体では原子レベルでの並進対称性がありませんので、運動量を明確には定義できません。
ただし長波長の波に対しては、連続体近似が使えるので保存する傾向にあります。
例えばガラス中でも可視光や長波長の音波は波として定義できます。
波長が長い場合(波数ベクトルが小さい場合)は、Umklapp過程はあまり起こりませんので、もう少し単純にしてわかりやすい例を示してみます。
外部から結晶に光が入射した場合を考えてみます。
そのとき入射する前の光の運動量と、入射後の光の運動量との間には部分的な保存則が成立します。
具体的には、入射面に垂直な方向については並進対称性がないために保存則が破れますが、入射面に平行な方向については波数ベクトルの保存則が成立します。
その結果、面に斜めに入射した波の向きが変わり、それが屈折や反射という現象に相当します。
これをより明快に表現する方法としては、波の位相速度を用いると便利です。
つまり媒質ごとの位相速度の違いによって波は屈折します。
古典電磁気学は、光の位相速度の違いを屈折率の違いという形でうまく表現しています。
弾性波でも同様に、媒質1での位相速度と媒質2の位相速度の違いを指定すれば、同様に弾性波の屈折を定義できます。
海の波も海底が浅くなると位相速度がおそくなり屈折し、結局、海岸に打ち寄せるときはほぼ海岸線に並行になります。
ただし、反射と屈折の比率や反射の位相などについては境界条件が必要です。
光については電場や磁場の連続条件で境界条件を与えられますが、フォノンの場合についてはミクロな力学が境界条件の設定に必要になるでしょう。
一方、波長が長い場合で入射面に垂直方向成分が保存しなかったときの全系の運動量(素粒子としての運動量)は、結晶全体が受け持つことになります。
つまり、素粒子としての運動量保存則は全系では成り立っています。
ただし結晶の質量は十分に大きいので、結晶が受け持つ運動量は無視してもかまいません。
しかし真空中に浮いている原子ひとつが光子を受けとる(吸収する)場合や放出する(発光する)は、無視できない大きさになります。
ある領域から外部に向かって出てゆこうとする原子は、ドップラー効果によって静止している場合の共鳴エネルギーよりも低いエネルギーのレーザー光を共鳴的に吸収し、それを四方八方に放出します。
そのため原子にわずかながら圧力をかけることができます。
この原理がレーザートラップとして利用されるわけです。
しかし光の波長が結晶の格子定数と同程度になると(つまりX線の場合)、入射面に平行な成分でも運動量の保存則は成立しません。
これは、X線のブラッグ反射でよく知られているように、回折が起こるからです。回折格子もその良い例で、直進する光とは別に、ある決まった角度に回折光が発生します。
このときは、波の運動量は保存していませんが、逆格子ベクトルだけ波数ベクトルが変化することに対応します。
言い換えますと、ブラッグ反射は、入射X線の波数ベクトルが逆格子ベクトルの分だけ向きを変えることに相当します。式で書くと以下のようになります。
k1 = k1' + Gj
テレビを見ていてふと思ったんですが、なぜ、テレビの前で手とかを早く動かすと飛び飛び(点滅してるみたい)に見えるのですか?
あと、テレビは1秒間に数十回点滅してるけど、人間が反応できるのよりも早いので、連続に見えているのですよね。
じゃあ、普段僕たちが見ているもの(電気以外のもの)つまり、太陽からの光で見えているものは連続して見えているのですがこれは、本当はすばやく点滅してるのですか?
もし、点滅してるとするとどれくらいの早さでしてるのですか?教えてください。(大学1年)
テレビでは525本の走査線を1画面として1秒間に30回描いています。
しかしブラウン管方式ではちらつきが感じられるので、奇数番目の走査線と偶数番目の走査線を交互に描いてちらつきを軽減しています。
つまり1秒間に合計で60画面を描いています。
高校の物理の教科書にもあるように、ブラウン管方式のテレビでは電子ビームを細く絞って蛍光面にぶつけて光らせていますので、瞬間瞬間に光っているのは電子ビームの当たっている一点だけです。
それが高速で画面上を動いています。画面全体が一度に光っているわけではありません。
光っている点が1画面を描き終えて次の画面を描くまでの間、ブラウン管は光っていません。
そのためにブラウン管の前で手を速く動かすと、一瞬一瞬のシルエットが次々と見えて指が何本もあるように見えます。
たとえば、ブラウン管テレビの画面を写真で撮るとシャッターが開いている間の部分的な画像しか写りません。
ブラウン管ではこのような不連続な光り方をしていますが、人間の目には残像効果があって次の画面が写るまで残像が目に残っていますから、ちらつきを感じるということはありません。
一方、最近普及してきたプラズマテレビや液晶テレビでは全面で同時に光っているため、手を速く動かしてもご質問にあるような点滅は見えません。
1秒間に30コマの画面が変化しながら次々と現れているにもかかわらず、人間にとっては物体がなめらかに動いているように見えることも残像効果と関係あります。
もともと、人間の網膜では動く物体をそれほど鮮明な画像としてはとらえていないので、テレビの不連続な画面でもそれほど気にならないのでしょう。
一方、映画館で上映するフィルム映画では1秒間に24コマの画像が次々と入れ替わります。
この映画をテレビで見るときは、毎秒24コマを毎秒30コマに水増ししていますが、気がつきませんね。
また西部劇で幌馬車の車輪がまるで逆回転しているように写ることがありますが、一瞬一瞬のタイミングのずれがそのような錯覚を起こさせます。
テレビの他にも不連続で光っているものはたくさんあります。蛍光灯では交流の電流が交互に流れるたびに光りますから50Hz地区では毎秒100回光っています。
夜景を双眼鏡で見るときに、双眼鏡をぐるぐると動かすと街灯やネオンサインの点滅が見えて大変きれいです。
最近はインバーター方式の蛍光灯が普及してきましたが、この場合は非常に高い周波数で点滅しているので、ちらつきを感じることはありません。
これらの人工的な光とは異なって、太陽の表面やろうそくの炎(明るく光っているのは赤熱されたススです)では連続的に光っていますので点滅はなく、どんな瞬間をとっても光っています。
つまり熱せられた物体では、その温度でほぼ決まるスペクトルの光(可視光線だけでなく、赤外線や紫外線もあります)が連続的に出ています。
その他にも蛍の光や夜光塗料の燐光、稲妻、レーザーや発光ダイオードの光などいろいろな光があります。
また人間の目(網膜)で光をどのように感じるのか、色はどうして感じるのか、画像をどのように認識しているのかなどなど考えるといろいろなことがあります。
なぜ自転車は止まっているとバランスを取ることが難しいのに、こいでいる間はなぜ簡単にバランスをとることができるのでしょうか??
自転車をこぐとタイヤに角運動量が発生することから、それは角運動量の保存と関係している気もするのですが明確な答えを出すことができません。(予備校生)
直線運動しているものにはそのまま運動を続け、運動の状態が変化するのをいやがる性質があります。いわゆる慣性の法則です。
交通標語の「車はすぐには止れない。」というコピーがそのことを言いあてています。
止めるためには、ブレーキをかけ大きな力が必要になります。
回転運動の場合にも同じことがいえます。回転している自転車の車輪は、回転の状態が変化するのをいやがる性質があります。
ただし回転運動は少し複雑で、(1)回転の早さと共に、(2)回転の軸の方向が変化するのもいやがります。
ここでは後者が重要です。そして回転の早さが早いほど、回転の軸の方向を変化させるには大きな力がいるようになります。
つまり自転車の車輪の回転が遅いと少しの力でも車輪の回転の方向が変りフラフラするが、早いと(手荒いことさえしなければ)車輪の回転の方向は変わりにくく、まっすぐに進む性質が出てきます。
質問に出てくる角運動量という言葉を使えば、以下のように言う事もできます。
(1)早く回っている車輪ほど、車軸方向の大きな角運動量を持ちます。 (2)車軸方向(ひいては自転車の進行方向)を変えるには、車輪の持つその大きな角運動量の方向を変化させる必要があり、大きな力のモーメントが必要となります。 (3)普通に走行している自転車にそのような力のモーメントは加わらないので、車輪の持つ角運動量は方向を変えず自転車もまっすぐに進もうとします。 (4)反対に、ゆっくり走行している自転車では車輪の角運動量が小さく、外からの少しの力でその方向が変化するためフラフラすることになります。
Is it not a violation of the said principle?
For the thermodynamics law
The thermodynamics law states that entropy or disorder/randomness increases with time. But in the very early stage , the Universe is made up of random particles, which later on clump together to form stars, planets, etc, i.e some order is present.
Is it not a violation of the said principle?
The structure formation in the universe is determined not only by the entropy S but by others, such as gravity. Gravity plays an essential role in the structure formation in the universe. Stars are formed as a result of gravitational collapse of diffuse gas. Galaxy is a system in which many stars, together with gas and dust, are gravitationally bound. In addition to the thermodynamics, the dynamical property is crucial for the structure formation. Magnetic fields can also create ordered structures; it has been considered that collimated, fast-moving plasma flows (so-called jets) emanating from black holes and baby stars are driven by magnetic fields.
就職者53名(民間就職50名、公務員3名)
これが理学部の修士課程終了した人の就職実績ですが、はっきりいってかなり悪いと思います。
確かに大学というのは就職するための予備校ではなく、勉強をするというところですから就職だけにこだわって考えるのはよくないことかもしれません。
しかし就職活動という言葉が存在しますし、大学を出たら自分で働いてお金を稼がなければならないので 、必然的に就職ということは重要視されるのは当たり前だと思います。
理学部の場合、中学高校の教師になる人が結構いますがそれは大学で勉強したことは全然いかされないでしょう。
生かすとしたらならどこかの企業の研究所に入るか、博士まで行って教授になって大学で研究するかのどちらかだと思います。
ただ企業の研究所に入って研究させてもらえるのも大学の教授になれるのも一握りの人です。また、
企業の研究所にも研究する範囲があるので素粒子などはまったく企業から相手にされません。
ポスドクもアカポスもものすごい倍率で落ちる人がかなりの人のはずです。ましてやノーベル賞なんて夢のまた夢です。
理学部物理学科に行って素粒子の研究職につくのがこんなに実現不可能に近いとは思ってませんでした。
理学部に行く目的がわからなくなりました。就職も他の学部に比べてきつい。研究者にもなるのが難しい。しかも素粒子なんかは教授以外に道が無い。
理学部に行く目的ってなんですか?教えてください。(高校生)
就職が「良い」「悪い」という場合に、様々な基準があると思われます。
どのような基準に照らして「悪い」とおっしゃられているのか不明ですが、一般的見地からは、本研究科の就職実績は全国的水準をはるかに上回っているものと考えられます。
しかし、「良い就職とは何か」といった問題は、1元的な価値基準で定まるものではないので就職実績だけから判断するのは大きな誤りです。
人生は長く高校時代に考えることとは全く別のことに興味を見いだし、大学・大学院で専攻を変えたり就職時さらには就職後にも職種を変えることはごくごく一般的です。
もしかすると貴君は10年後には素粒子物理学とは全く異なる分野の仕事をされているかも知れません。
しかし、もしも素粒子物理学研究よりも、よりあなたの適性に沿う専門領域があるとしたらそれを見いだしてもらうこと、それこそが大学・大学院教育の主目的なのです。
個人的経験に照らしても周囲の人々の話を総合しても、高校時代に考えることは極めて限定された知識のもとでの狭い狭い将来像でしかないことが多いです。
私も高校時代は物理学には素粒子理論と宇宙論しかないと思っていましたが、それは全くの誤りでした。物理学はもっともっと巨大な学問です。
物理学に興味をお持ちなら、是非大阪大学理学部物理学科に入学して、その広大な研究の地平を見渡す冒険に参加してみてください。
細かい個々の専門分野のおもしろさは講義やゼミを通じてお教えします。研究者の道を選ぶかどうか、企業に就職するか大学で研究するかどうかなどは、そのような冒険をしていく中で意志が固まっていくことでしょう。
そして大阪大学は、そのような適切な進路指導を行うことができる体制が整えられています。
大学院から別の研究科、場合によっては別の大学の大学院に進学することも推奨されています。
あらゆる専門領域のトップレベルの研究者・教授の「品揃え」により、適切な進路指導が可能であることが、総合研究大学院大学たる大阪大学の強みです。
高校生の段階から、いろいろな情報を集め、分析し、ここにも投稿されるというあなたの行動力には本当に感心させられます。
是非とも大阪大学に来て欲しいと思います。しかし、あまり高校生の段階から、その時の状況・情報だけから判断して将来について狭く考えることをしないでください。
ダイナミックに進路を切り開いていくこと、それがこれからの若い人々に期待される人生像ですし、それが可能になったのは日本でも本当に最近のことです。
それは新たに獲得された権利なのです。是非存分に行使していって頂きたいと思います。
このような多様な価値観が渦巻く社会の中で、理学部とその出身者が果たすことのできる役割とは何かを考えてみますと物事を根本的・抽象的・大局的な観点から系統的に捉えることにより問題の解決を行う、ということが挙げられると思われます。
具体的な理学の知識が直接問題の解決につながることはもちろんのこと、それ以上により広い範囲の理学を越えたあらゆる分野において、理学的な発想・視点が重要な役割を果たす場合が少なくないのです。
理学部出身で現在理学に直接関わる職種についていない人でも、そのような方々のお話でよく聞くのは「理学部出身でよかった」ということです。
前の教育審議会の主要メンバーである某小説家は、「私の人生において方程式など何の役にも立たなかった。方程式など知らなくても生きてこれた」といった趣旨の発言をされていましたが、これは教育に関わる公人の発言としては全く見識に欠けるものと言わざるを得ません。
むしろ常に世界のどこかで続いている戦争・紛争、もしくは、カルト宗教や、インチキ商法などの跳梁跋扈を見てもわかるように、政府、市民の合理的な判断力が大幅に低下している昨今にあっては理学的な発想を持つことは、今後人類が合理的に振る舞うための最後の砦と言っても過言ではないでしょう。
「方程式が人生に役に立たない」という発言は、物事を根本的につきつめて考えるという姿勢に対する、有史以来の「人間が陥りやすい安易なイデオロギー」からの攻撃を象徴しています。
ガリレオの宗教裁判の話はご存知かと思いますが、理学はずっとずっとそのような闘いを勝ち抜いてきました。
その強さが、その発想・思想・方法の正当性を雄弁に物語っています。もしも貴君が小中高校の夏休みの自由研究などを通じて、「何かに興味を持って、調べて、新しいことを発見する」ことにすでに喜びを見いだした経験があり「研究っておもしろそうだなぁ」と思っておられるならば、研究者として最も大切な適性の大半をすでに持っていることになります。
最近の風潮では、すぐにビジネスに結びつく近視眼的な応用研究のみがもてはやされて理学部に対する不当な風当たりも強いのですが、理学に興味をもたれた貴君のような貴重な同志には是非この長い長い研究の歴史に新たなものを付け加えていく活動に参入して欲しいと願っています。
最後に、上記の小説家の発言に対しては、同じ小説家である村上春樹氏の「ノルウェイの森」の中の一節を引用して答えとしたいと思います。
おそらく村上氏は理学の専門教育を受けたことはないかと思われますが、理学的視点・発想の重要性を直感的に理解されているのだと思います。
「ねぇワタナベ君、英語の仮定法現在と仮定法過去の違いをきちんと説明できる?」 と突然僕に質問した。
「できると思うよ」
と僕は言った。
「ちょっと訊きたいんだけれど、そういうのが日常生活の中で何かの役に立ってる?」
「日常生活の中で何かの役に立つということはあまりないね」
と僕は言った。
「でも具体的に何かの役に立つというよりは、 そういうのは物事をより系統的に捉えるための訓練になるんだと僕は思ってるけれど」
貴君の今後のご健闘とご発展をお祈りします。
先日”物理化学”の授業で、「シュテルン・ゲルラッハの実験」を習いました。
それによると“Ag(銀)は磁界を通ると、2本の輝線になり、それはスピンの持っている磁気量子数によるものである。
つまり、Agの不対電子は1個なので、スピン多重度が2になる”ということらしいのです。
Cdは不対電子がないので、不均一磁場を通っても2本に分かれることがないのは分かります。
まず、発光スペクトルというのは輝線と同じことでしょうか?
教科書にはNaは589.0と589.6nmに2本の発光スペクトルを示すと書いてありました。
Na原子は不対電子が1つなので2本の発光スペクトルを示すのですか?
それと、教科書にはH原子のスペクトルは一本の発光スペクトルである、とも書いてありました。H原子の不対電子は一つなのになぜ1本なのでしょうか?
NaとHでスペクトル数が異なるのはなぜなのでしょうか?
物理化学の先生は「系列がどう」とかおっしゃっていたような気がするのですが、説明がよくわかりませんでした。
どうぞよろしくお願いします。
複数のことを質問されていますので、それぞれ分けて説明します。
詳しくは、原子物理学や原子スペクトルを扱った本を読んでください。
たとえば大きな磁石のN極付近を考えてください。
その極に近づくほど強い磁場が発生しています。そこに、別の小さな磁石を置きます。
そのとき小さな磁石のS極を大きな磁石のN極に面するようにして近づけると引力が働き、N極側を面するように近づけると斥力が働きます。
さて中性の銀原子は、基底状態ではスピン角運動量1/2を持っています(小さな磁石と考えてください)。
このスピン角運動量は銀原子の最も外側を運動している電子(5s電子と言います)によるものです。
このとき量子力学的効果によってアップスピンとダウンスピンのふたつの状態ができています。
これを磁場中に置くとゼーマン効果によってエネルギー的にも異なる状態になります。
このアップスピンとダウンスピン状態では磁石の向きが違いますから、シュテルン・ゲルラッハの実験のように場所によって強度が変化している磁場中に置くと、上述のように磁場から受ける力の向きが違います。
そのためアップスピンとダウンスピンの状態のビームの向きが互いに異なり、銀原子が到着する位置がずれることになります。
ナトリウムの中性原子も銀原子と同じように基底状態ではスピン1/2を持っています(最も外側を運動している電子は3s電子と言います)。
シュテルン・ゲルラッハの実験を行えば、ナトリウムの中性原子のビームもふたつに別れます。
一方、発光の場合は励起状態を考えなくてはなりません。
原子の励起状態はたくさんありますが、それがエネルギーの低い状態に遷移するときに光を出します。
原子の状態の中には、原子核に対して回転運動をしている電子(量子力学では軌道角運動量を持つ電子ということになります)があります。
つまりスピン角運動量1/2だけでなく、軌道角運動量をもっている状態があります。スピン角運動量を電子の自転にたとえると、軌道角運動量は原子核の周りを回る公転運動にあたります。
このとき公転運動の回転の向きに対して、アップスピンとダウンスピンの二通りの自転状態が考えられます。
実は、その状態のエネルギーがわずかに違います(これは磁場が無くても分裂しています)。
この分裂を引き起こす相互作用は、スピン軌道相互作用と言います。これは電子の原子核に近い側と遠い側で原子核から受ける引力が違うために、 自転運動の違いがエネルギーにも影響するためです。
具体的には、ナトリウム原子の励起状態のひとつとして、スピン角運動量1/2と軌道角運動量1をもった3p状態というのがあります(ただし、正確には、全ての電子を含めて指定しなくてはならないので、ここで言う電子ひとつの状態で原子状態を指定するのは、厳密ではありません。ここでは便宜的に利用しています)。
その結果、スピン角運動量1/2と軌道角運動量1 をもった場合では、自転と公転の向きが同じ状態として全角運動量が3/2、逆向きの状態として全角運動量が1/2があり、エネルギー的に分裂します。
もし磁場があると、全角運動量が3/2の状態はさらに4つ、全角運動量が1/2の状態はふたつに分裂します。
磁場がない状態で考えると、ナトリウム原子の3p励起状態から3s基底状態に遷移するときに、589.0と589.6 nm の二種類の波長の光を出します。
これはナトリウムD線といって、オレンジ色をしています。トンネルの中でよく使われるナトリウム灯の色です。
要するに、ナトリウムD線の分裂はスピン軌道相互作用で分裂した全角運動量が3/2と1/2の状態が基底状態へ遷移するときの発光です。
ご質問の答としては、シュテルン・ゲルラッハの実験でビームがふたつに分かれるのは、基底状態の原子におけるアップスピンとダウンスピン状態の違いです。
一方、ナトリウムD線の分裂は磁場は関係なくて、励起状態におけるスピン軌道相互作用によるもので分裂の原因は別々です。
ただし、量子力学での角運動量の考え方を基礎にしているという意味では共通性があります。
さて、スピン軌道相互作用の大きさは重い原子ほど大きくなり、分裂エネルギーも大きくなります。
それは、原子核の引力が大きい原子(つまり陽子の数が多い重い原子)ほど、電子の原子核に近い側と遠い側とで、原子核からの引力の差が大きくなり、自転と公転の相互作用が大きくなるためです。
たとえば、ナトリウム原子と相似形の電子配置をしている中性のアルカリ金属原子(Li, Na, K, Rb, Cs)は、順にスピン軌道相互作用が大きくなり、ナトリウムD線と相似の分裂(p状態の分裂)はこの順で大きくなります。
ここで比較している発光の遷移は、Li, Na, K, Rb, Cs 順に 2p→ 2s, 3p→3s , 4p→4s , 5p→5s , 6p→6sです。
最も軽い水素原子では、2p状態の分裂 は非常に小さくなります(ただしゼロではありません)。
水素原子では、1s, 2s, 2p, 3s, 3p, 3d, ・・・という量子準位があります。観測する遷移としては2p→1s が可能です。
しかし、1pというのはありませんので、1p→1s とうのはありません。2p状態の分裂が小さいために、普通の分光装置では見ることができないためにスペクトルが1本になっているとしているわけですが、十分な分解能の装置では、分裂しているのがわかります。
ちなみに水素原子での2p状態の分裂はナトリウム原子の3p状態の分裂の約50分の1程度で、10万分の4 eV です。
重い原子のCsの6p状態では分裂は100 分の6.8 eV です。中性の銀原子の 5p 状態では 100分の 11.4 eV です。
また原子核はスピンを持っていますので、それと電子との相互作用によって更に分裂します。より精密な測定をするとそれも見えてきます。
たとえば、ナトリウム原子の原子核スピンは3/2ですの、4つの状態が含まれています。
これと上記の3s電子との相互作用を考えると、アップスピンとダウンスピンの状態はそれぞれ4本づつに分裂します。
これは超微細相互作用と言います。
同じ強さの磁石を二つくっつけると、一つのときより強くなりますか?
まず、磁石の強さというのは、いったい何のことを言えばよいのかを考えてみましょう。
磁石にはいろいろな形がありますので、ここではN極とS極が対になっている棒磁石[N=S]を考えて説明します。
N極どうしやS極どうしはくっつきませんが、N極とS極はくっつきます。
磁石の強さを調べるために、鉄棒を近づけてみます。すると、N極とS極の近くでは強くくっつきますが、NとSのあいだのところではくっつきません。
これはN極から磁力線(じりょくせん)が出ていて、S極に集まって吸いこまれていると考えると良いでしょう。
このとき、N極とS極の近くには磁場(じば)が集中します。
磁場は目に見えないけれど、鉄棒はそれを感じて磁石になるからです。
磁場の向きを矢印で示すと下のようになります。
→
→ →
↑ ↓
←[N=S]← [(N)鉄棒(S)]
↓ ↑
→ →
→
次は、棒磁石をふたつくっつけてみます。棒磁石のくっつけかたはいろいろありますね。ひとつは、直列です。つまり同じ向きでくっつけると
[N=S][N=S]
このとき、磁場の様子を書いてみましょう。
→ →
→ → → →
↑ ↓↑ ↓
←[N=S]← ←[N=S]←
↓ ↑↓ ↑
→ → → →
→ →
この図で、矢印が↑↓になっているところは互いに反対向きの磁場がいっしょになっていますから、磁石を近づけると消えてしまいます。
そのまわりでもほとんど消えてしまいます。
つまり、磁石を近づけると次のようになります。
→
→ →
→ →
↑ ↓
←[N=S]←[N=S]←
↓ ↑
→ →
→ →
→
ふたつの棒磁石のあいだでは、磁力線はN極から出てすぐにS極に吸いこまれます。
そのために磁場は外側はでてこなくなります。
三つや四つの磁石を次々とくっつけてもおなじです。
→ →
→ →
→ →
↑ ↓
←[N=S]←[N=S]←[N=S]←
↓ ↑
→ →
→ →
→ →
つまり、磁石をいくつ繋げても両方の端っこの磁場の強さは変わりません。
鉄の棒を近づけるとしらべることができます。
だからといっていくつ磁石をくっつけても強さがかわらないと考えるのは正しくありません。
よく見て下さい、磁場が遠くまで広がります。
もっとも大きな磁石は地球です。地球上の多くの場所では磁場が南北に向いています。羅針盤(らしんばん)はそのことを利用して、磁石の針がいつも南北を示すことを使っています。
太陽から飛んでくる電気をもった粒子は、この地球の磁場で大きく曲げられて北極と南極に到着し、オーロラの光を発生します。
こんどは、磁石を並列にしてみます。
→
→ →
↑ ↓
←[N=S]←
↓ ↑
→ →
→
←
← ←
↓ ↑
→[S=N]→
↑ ↓
← ←
←
磁石をもっと近づけて、さっきと同じように考えると
→
→ →
↑ ← ↓
←[N=S]←
↓ ↑
→[S=N]→
↑ → ↓
← ←
←
となりますが、もっと近づけると
↓←[N=S]←↑
↓→[S=N]→↑
となります。磁石が打ち消し合って、N極とS極のすぐ近くのせまいところだけ磁場が残ります。
ひとつひとつの磁石は変わっていませんが、磁場がせまいところだけでまわりに広がっていません。
ですから、遠くで磁石の磁場を感じることができなくなります。
これを磁石が弱くなったと思うこともできますがひとつひとつの磁石は弱くなっていません。
鉄はとても小さな磁石が色々な方向を向いて集まっています。
お互いに打ち消し合って外には磁場がでてきません。ですから、鉄と鉄はくっつきません。
しかし強い磁石に鉄を近づけると、鉄の中の小さな磁石は同じ向きに揃います。つまり、鉄も磁石になります。
鉄が棒磁石にくっつくのはそのためです。もし、とてもつよい磁場の中に鉄を置くと、鉄の中の小さな磁石が磁場の方向にそろったまま、元にどらなくなります。
すると鉄は自分で磁石になってしまいます。磁石はそのようにして作ります。
このように、最初は磁石になっていなかったものを磁石にすることを着磁(ちゃくじ)と言います。
普通の鉄は、あまり強い磁石にはなりません。
最近、世界でもっとも強い磁石「ネオマックス」が日本で発明されました。モーターやコンピュータなどで使われています。兵庫県西播磨のSPring-8(スプリングエイト)では、ネオマックスの磁場で電子を波のように次々と曲げて、さらに強い光を発生させるのに使っています。
このような説明もおもしろいけれど、もっともっと大切でおもしろいことがあります。
それは棒磁石と鉄棒をかりてきて、自分で実験をしてみることです。何か発見したら、教えてください。
鉄棒は釘でも大丈夫です。
空気抵抗があるんなら質量が大きいほうが抵抗も大きくなるような気がします。
インターネットで色々調べてみたんですが難しい式が書いてあってよく分からないです。よろしくお願いします。
ご存じのように、真空中では空気抵抗がないので物体の落下速度は重力加速度の割合でどこまでも増加します。
ここで座標を上向きを正とすると、重力加速度は下向きですから負の値 -g を与えることにします。
すると、重力は質量 m と重力加速度 -g の積 -mg で与えられます。一方、質量 m と加速度a の積はその物体に働く力に等しくなりますから、
ma = -mg
となります(運動の第二法則)。このとき、両辺に m がありますか ら、a = -g になって、加速度は質量 m に依存しないわけです。
その結果、物体の落下速度 v は時間 t に比例してどこまでも加速していきます。
式で書く と v = -gt となります。
しかし、大気中では空気抵抗(粘性抵抗)k を受けます。その力は上向き(重力と反対方向)ですから、正の値 k とします。すると、力の関係は
ma = -mg + k
となります。ここで k は落下する物体の形や大きさや速度が決まれば物体の質量には依存しません。
それは物体が空気と接するのは物体の表面だけですので、同じ速度で落下する場合は物体の内部に隠されていることには関係しません。
つまり外形が等しければ質量によらず空気抵抗も等しくなります(しかし、次に述べるように速度に依存します)。
空気抵抗 k は静止した物体には働きませんから速度の関数です。もし物体の速度 v が低くて k が v に比例すると近似できる場合は k = nv と書くことができます。
ここでn は落下する物体の形や大きさや空気の粘性で決まる係数です。n が大きいほど空気抵抗が大きいことになります。
すると、力の式は
ma = -gm + nv
となります。速度 v が一定になる終端速度では速度が一定になり、これ以上加速しませんから a = 0 です。
これを代入すると、v = gm/n となって、 質量の大きい物体ほど早く落下します。 逆に言うと、質量が大きい方が落下速度が速いので大きな空気抵抗を受けて、それが大きな重力とバランスを取るわけです。このことから、重い物体ほど速く落ちるという経験則を導きますが、それは空気抵抗があるためです。ガリレオは、空気抵抗が無視できる場合においては落下速度は質量によらないこと、つまり「慣性の法則」を導きました。そのときに多くの実験事実に基づいて結論を導いていることに注目しなくてはなりません。ケプラーの天体観測も同様です。ニュートンは数学を用いてこれらの事実を力学の体系として完成しました。
さて、物体の速度がゆっくりのときは、空気抵抗は速度に比例しますが、それはかなりゆっくりとした速度です。たとえ ば、シャボン玉が落下する場合や、霧雨ていどの小さい雨粒については成立します。しかし、少し早くなると速度の二乗に比例します。ピンポン球や野球のボールや普通の大きさの雨粒が落下すると きは、空気抵抗は速度の二乗に比例します。式で示すと、
ma = -gm + bv^2
となります。ここで b は速度の二乗に比例する抵抗で、
b = CD*r*A
ここで、A は物体の断面積、r は空気の密度、CD は物体の形で決まる数値で、球形では 0.3 程度の値になります。終端速度は v^2 = gm/b です。ピンポン玉程度の大きさの氷だと時速 100 km 程度の速度になりますので、この大きさのヒョウが体に当たると大ケガをします。もし、全ての速度を一緒に考えたい場合は、
ma = -gm + nv + bv^2
とすればよいでしょう。もっと早くなると乱流が発生したりします。
また 「球(半径15mm)が空気(常温・1気圧)中を速度v〔m/s〕で運動するときの空気抵抗の近似式を調べています。」の質問もご覧下さい。
大阪大学には理学部のほか、基礎工学部、工学部があり、良く似た名前の学科がありますが、どこがいったい違うのでしょうか。また、物理も化学も、原子や分子を扱っていますが、学科の境界はどこにあるのでしょうか。
これはよく受ける質問で、大阪大学としても各学科の特色の紹介に力を注いでいるところです。例えば、以下のサイトをご覧ください。
大阪大学をもっと知りたい受験生のためのサイト:
https://www.osaka-u.ac.jp/sp/entrance/
工学部と理学部の関係について紹介するyoutube動画:
https://www.youtube.com/watch?v=ZQ2SHTFZ8Bs
さらに詳しく知りたい方は、興味ある研究室に連絡を取って見学に来るなどしていただけると、より具体的に雰囲気がわかるかなと思います。
宇宙人や地球外生物の研究が出来ますか。
宇宙物理側からは例えば宇宙において有機物質の生成がどこで・どのようにして行われるのかという形で生命の起源解明につながる取り組みがなされています。より広い視点で見ると、宇宙の化学進化(宇宙における多様な元素・分子がどのようにして生成され、ばら撒かれているか)を明らかにすることも生命の起源を解き明かす重要な鍵と言えるでしょう。このように宇宙物理学の観点から生命の起源を探る取り組みができ、阪大の宇宙地球科学専攻では関連する研究が多角的に進められています。より詳しくは、以下の専攻HPをご覧ください。
宇宙地球科学専攻HP 専攻・研究分野紹介
http://www.ess.sci.osaka-u.ac.jp/about/intro.html
http://www.ess.sci.osaka-u.ac.jp/about/research.html
将来宇宙開発関連の仕事につきたいのですが。
宇宙探査に関する研究を行っている研究室もありますし、阪大理学部では、そういった分野を身近に感じることができると思います。卒業生で衛星ビジネスや設計などを行う会社に進んだ人もいます。簡潔に言えば、もはや宇宙開発は様々な形で世界的ビジネスとなっているので、仕事にするかどうかはあなた次第とも言えます。
参考までに、阪大の宇宙地球科学専攻で行っている宇宙探査に関する研究については、こちらからご覧ください。
宇宙地球科学専攻HP 研究分野紹介
http://www.ess.sci.osaka-u.ac.jp/about/research.html
化学について
将来、化粧品会社で研究・開発に携わるにはどのような学科を選べばよいですか?
また、そのような会社に就職している実績はありますか。
化粧品会社で研究・開発というと、かなり広い分野が当てはまります。 材料・分析関係は化学でしょうし、安全性関係は医学・薬学・生物学がメインとなります。 化粧品はイメージで売るところも大きいので色やデザインなどの美術的センスも必要ですし、理系のみで研究開発が行なわれるわけではありません。 とはいえ、人員は化学系の学科の卒業した人が最も多いでしょうから、まずはここかと思います。 当大学の理学部ですと化学科が相当します。
化学科では、すぐ浮かぶような有名な化粧品会社でもこれまでに何人も卒業生が就職しています。また、生物科学専攻でも、毎年数名が修士修了後に化粧品会社の研究・開発職に就職しています。ただ、化粧品会社で大きな研究・開発部門をもっているところは多くないと思われ、やはり化学メーカーの方が研究開発に携わる人数が圧倒的に多いので、化学科ではそちらに就職する学生が多いです。
どの学部を受験するか迷ったときは、大学に入ってから何を中心に学びたいかについて考えてみると良いでしょう。例えば薬学部では、基礎となる化学、生物学、物理学に加え、免疫学や薬理学、生化学なども学ぶことになるでしょう。
大阪大学理学部では、化学科に入学しても、化学だけでなく数学、物理学、生物学、地学の基礎をまず学ぶことになります。大学や学部によって、学べることだけでなく出会う人も変わってくるでしょう。将来に対する考え方も変わるかもしれません。ホームページやオープンキャンパスなどでカリキュラムや学生生活等の情報を入手したり、在学生の話を聞いたり、雰囲気を肌で感じるなどして、志望校・学部を考えると良いでしょう。
なお、理学部の卒業生は、教育職や研究職に限らず、幅広い分野で国際的に活躍しています。理学部で身につけることのできる基礎知識、課題発見力、柔軟な発想力、的確な判断力などは、社会のどの分野でも求められる力です。
原子は原子核の周りを電子が回っているとなると、人間の手のひら(あらゆるものも)は表面が電子で覆われている状態になるということになるのですか?
もし、そうだとすればなぜ握手ができるのですか?
ほんとうなら、斥けあって手と手を握ることができないのじゃないのでしょうか?
もっというと、あらゆるものと触れることができないのじゃないのでしょうか?教えてください。
ご質問は素朴な内容でありながら、非常に深い意味が含まれています。
どうして握手ができるのかを理解するためには、いくつかのことを考えなくてはなりません。
[中性の原子同士の間には、電気的な力は発生しません]
学部にもよりますが、大学では電磁気学を勉強することと思います。
その中にガウスの法則が出てきます。原子に含まれる電子のように、球形に分布した電荷は外部から見ると球の中心に全ての電荷が集まったのに等しい電場が発生します。
中性の原子では、電子と同じ数の陽子が原子核に含まれていますから電子の発生する電場と原子核の発生する電場は完全に打ち消しあいます。
その結果、中性原子の外側では電場は消えてしまいます。
したがって、中性の原子同士の間には力はほとんど発生しません(量子力学的な揺らぎによって非常に弱い引力は発生しますが)。
ですから、手と手の間には、接触するまで力は発生しません。
ただし、原子の内側では、原子核からの電場が強く働いていますので、原子の内側にいる電子は原子核に強く引きつけられています。
イオンではどうでしょうか。たとえば、ナトリウムの陽イオンでは、電子の数が陽子の数よりひとつ少なくなっています。
その結果、イオンの外から見るとプラス1価の電荷が原子核の位置にあるような電場が発生します。
陰イオンでは、逆にマイナスの電荷が原子核の位置あるような電場が発生します。
ですから、NaCl結晶では隣接するナトリウムのプラスイオンと塩素のマイナスイオンの間に比較的強い引力が発生します。
しかしブラスとマイナスの電荷は同数ありますので、もっと遠くからみるとそれらの電場は互いに打ち消しあいます。
ですからNaCl結晶では表面の近くだけで電場が発生し、遠くでは電場はほとんど発生しません。
実際、食卓塩の粉末は互いにくっつくことはありません。ただし、湿気があると水分が仲立ちになってくっつける作用がありますので、湿気るとベトベトしてきます。手の皮膚を構成する原子も中性のものだけではなく、プラスやマイナスのものもありますがNaClと同様に全体としては中性ですので、遠くでは打ち消しあって力は発生しません。
これでご質問の答えになっていると思いますが、実は以下に示すように握手できることにはもっと深い意味があります。
[粒子には同じ場所・状態にいられるボーズ粒子といられないフェルミ粒子があります]
基本的な粒子(素粒子)には大きく分けて二種類あります。
ひとつはボーズ粒子と呼ばれるもので、同じ場所に同じ状態でいることができます。例えば光子です。
もうひとつはフェルミ粒子です。この粒子は同じ場所に同じ状態でいることはできません。例えば電子や陽子などです。
この性質によって、非常に大きな違いが発生します。
真空中で二つのレーザー光線をぶつけたら何が起こるでしょうか?何も起こらないで、通り抜けてしまいます。
これは、光子はボーズ粒子だからです。したがって、光で光を曲げたりすることはできません。
スターウォーズのライトセーバーは、実はこの原理に反します(だから面白い)。
ところが、フェルミ粒子である電子は同じ場所に同じ状態でいることはできませんから、もし無理矢理に二つの原子を押しつけあうと非常に大きな斥力が発生します。
それは、片方の原子に含まれる電子は、もう片方の原子の電子のいるところに進入できないからです。
たとえば二つのヘリウム原子を互いに近づけると、それぞれのヘリウム原子に含まれる2個の電子同士は互いに退けあいます。
無理に近づけると原子は壊れてしまいます。
手の皮膚の表面を構成している原子も同様に、互いに接すると退けあいますから握手できることになります。
もし、電子や陽子や中性子がボーズ粒子でできていたら握手できずにすり抜けてしまうかもしれません。
同様に我々は地上に立っていられないことになり、地球の中心まで落ち込んでしまいます。
さらに、これらのことは電子が結晶中を自由に動けるのかどうかに深く関係してきます。
たとえば、銅もNaClも共にたくさんの電子を含んでいます。
しかし、銅では電子が自由に運動して金属になり、NaClでは動けずに絶縁体になります。
これらはフェルミ粒子である電子のなせる性質です。
[電子を共有すると強い結合が生まれます]
今度は、二つの水素原子を近づけてみます。水素原子は原子核(陽子1個)と電子1個でできています。
実は電子にはスピンというものがあります。これは電子の自転と考えることができます。
そのとき、右回りの自転と左回りの自転という二つの選択肢があります。そのために水素原子において陽子の周りを回る電子の状態には、右回りと左回りの自転をした二つの電子が入ることができます。三つ目はだめです。
そのために二つの水素原子を近づけると、互いの電子は一緒の状態をとり水素分子として安定な結合状態ができあがります。
同様に、酸素や窒素原子同士も結合してそれぞれ酸素分子や窒素分子が安定になります。
これらの結合では、互いに電子を共有しますから共有結合と呼ばれます。
これは非常に強い結合で、我々が手にする堅い物体の多くは共有結合でできあがっています。
それ以外にも金属結合や水素結合などいくつかの結合が知られています。
我々の手の皮膚を構成する原子は、このような結合によって結ばれ形が保たれています。
アクセサリーの24金メッキを綺麗に剥がしたいのですが、サイズが大きく、複雑な形状なので研磨で剥がすのは大変です。
●24金メッキしてあるものを王水(硝酸1:塩酸3)につけたとして金が溶けるという他に何か危険な反応が起こりますか?(熱とか気体が発生するとか)
●メッキの中身は亜鉛なのですが、中身に王水がつくとどういった反応が起こりますか?金だけうまく剥がす方法はありますか?
●王水を作るため濃硝酸と濃塩酸を混ぜるときに、何か危険な反応が起こりますか?
●これらの作業を自宅でするときの注意点は何かありますか?
王水は非常に酸化力の強い溶液であり、金を溶かすことができることで有名です。
しかし、ご質問のような亜鉛の表面の金メッキ膜だけを溶かすという作業には残念ながら使えません。
その一番の理由は、亜鉛のほうが金より王水に溶けやすいということです。
つまり金膜だけを溶かそうとしても、金めっきが溶けた部分あるいは金膜に開いた細かい穴からも下地の亜鉛が王水によって溶け出してしまうからです。
イオン化傾向という言葉をご存知だと思いますが、亜鉛のほうが金に比べてイオンになりやすい性質をもっています。
つまり亜鉛のほうがイオンになって溶液に溶け出しやすいため、王水とも激しく反応します。
この反応は金と王水との反応より速く起こるため、金を溶かそうとして王水にアクセサリーを入れると亜鉛の本体が部分的に激しく反応して溶け出し、本体が侵されて形が崩れてしまうと予想されます。金膜も一 部は溶け出すかもしれませんが、金膜だけを溶かし出すことはできません。
王水は非常に酸化力が強いため、取り扱いが非常に危険な薬品です。とくに御質問のアクセサリーでは、亜鉛が王水と激しく反応することが予想されます。反応が起こると溶液の温度が上がり、これによりさらに反応が速くなるため有害な二酸化窒素などの気体の発生も激しくなり非常に危険です。
また、王水を作るために用いる硝酸、塩酸も劇物に指定されている試薬です。したがって、王水の調製や取り扱い、廃液の処理などは自宅でできる作業ではありません。
また、高校の理科室でも十分 な設備があるとは思えませんので、王水の取り扱いは困難です。
作業には、相当の化学の知識と経験のある人が付き添う必要があります。絶対に一人では行なわないでください。
化学は大変面白い学問で、いろいろな物質について実験してみたいという興味は大変素晴らしいと思います。
しかしながら化学薬品の中には大変危険なものもあり、そのような薬品については将来十分な知識と経験を積んでから取り扱ってください。
大学で食品の栄養素など天然高分子の研究をしたいと考えています。大阪大学の理学部では生物科学と化学のどちらの学科がいいのでしょうか。
もし化学科だとしたら、化学科では物理が重要と聞きますが、受験で生物を選択した私でもついていけるのでしょうか。
現在、化学と生物学の境界はかなりぼやけてきており化学者と生物学者の両方が同じ分野を研究することも多くなってきています。
研究したいと考えている食品の栄養素や天然高分子は、まさにそのような境界領域の分野だと思います。
あえて違いを挙げるならば、栄養素や天然高分子そのものの性質や化学変化について調べるのが化学、 栄養素や天然高分子によって人体がどのように応答するかを調べるのが生物学だと言えるかも知れません。
ただし栄養素や天然高分子が人体に与える影響を追求していくと、それらの化学的性質をよく理解しておくことが必要でそれには化学の知識が不可欠になります。
化学を習得するには、物理の素養も必要ですが現在化学科に入学してくる学生さん の約1/3は、高校のときに物理を選択していません。
入学後は物理の講義もとる必要がありますが、高校で物理を選択していない学生さん向けの物理の授業を開講していますのでそこで高校で習っていなかった分を補うことができるようなカリキュラムになっています。
理学部は工学部などに比べて就職が厳しいと聞きましたが、大学院まで進んだ場合はどうなのでしょうか?
よく「理学部や理学研究科は就職”無理”学部」などと言われているようですが、断じてそんなことはありません。
大阪大学理学部および理学研究科では、数学・物理学・化学・生物科学の幅広い知識はもちろんのこと、複雑な自然現象を司る原理・原則、さらにそれを基盤とした論理的思考についてしっかりと学んだ上で、世界の最先端の研究を行っています。
企業でも新しい技術や製品の開発をする際には、複雑な事象の中から本質的な問題を抽出し解決する能力が求められます。企業への就職先については、工学部のように特定の業種に限定することはありませんが、理学部/理学研究科の卒業生は幅広い素養をもつ人材として多方面から期待されており、毎年たくさんの求人が全国の企業や国の機関、高等学校などから届き、巣立って行きます。
大阪大学では、理学部の卒業生の2~3割程度が企業や高等学校教諭などに就職し、残りの7~8割程度が大学院の博士前期課程(修士課程)に進学しています。
大学院博士前期課程の修了者(修士)の7割程度が企業や高等学校教諭や国家公務員などに就職し、1~2割程度が大学院の博士後期課程に進学しています。
博士後期課程で博士(理学)の学位を取得した方は、大学教員や研究所の研究員や企業の研究開発スタッフとして活躍しています。
理学部化学科の先生から、化学科でも製薬、または創薬の勉強ができるという話を聞きました。
大阪大学理学部でも、そういった勉強ができますか?
また理学部のある大学なら、どの大学でもできますか?やはり薬学部のほうがいいのでしょうか?
製薬や創薬には化学の基礎知識が不可欠です。
その意味では、大阪大学理学部化学科では、製薬に関係する化学を学ぶことができます。
化学の中でも、特に有機化学や 分析化学は有機化合物である薬を合成したり、分析したりするときには必ず必要になります。
また、四年生や大学院生になると研究室に入って化学の実験を行うことになります。
薬そのものを合成する機会は少ないと思いますが、有機化合物の合成に必 要な実験を行う機会も多いので製薬研究に必要な知識や技術を習得することができます。(他大学の理学部化学科でも、同様な科目は学べるはずです。)
理学部と薬学部のどちらが良いかは、中々難しい問題です。現在使われている薬のことならば薬学部の方が詳しく学べるでしょうが、新しい薬を開発するときなどには理学部で学べる化学の基礎が重要になるのではないかと思います。
実際に、大阪大学理学部化学科の卒業生で製薬会社に就職した人も多くいます。
<物質は何と何でできている>など、この世に存在しているものは<どういう原子でできている>まで分かっているのに、炎はなんだろう?と思いました。
しかしどの資料をみても、炎については温度によって色がちがうということなどしか書かれていません。よろしくお願いします。
炎は、マイケル・ファラデーという19世紀の大科学者が毎年クリスマスに子供たちに向けて行われた科学講演会でも取り上げたテーマなのです。
講演の様子は、翻訳されて本になっているので是非読んでみてください。「ロウソクの科学※」という本です。
タイムマシンがあったらあなたを講演の行われた1860年に連れて行ってあげたいくらいです(本当はファラデーが行った講演会のようなことを僕ら科学者・教師が日本でもするべきなんですが)。
ファラデーは、その講演の中で日本のろうそくを紹介しているんですよ。当時の日本のろうそくは芯に工夫がしてあって、すすが出にくかったのだそうです。
19世紀にも高性能なMade in Japanがあったとはおもしろいですね!
またファラデーは、ベンゼンという石油工業にはなくてはならない物質を初めて発見したほか、電気や磁石についての大発見をしています。
この発見は、現在でも、物理という理科の一分野の大変重要な基礎になっていて、テレビ、ケータイ、電子レンジその他あらゆる電化製品はその発見がなければ存在しなかったといってもよいほど大切なものです。
おそらく高校の物理で習うと思います。当時ノーベル賞があったら、3、4回受賞していてもおかしくないほどの偉い科学者ですね。
でもファラデーは14才で製本屋に奉公に出されたために、独学で科学を学んだという人なのです。すごいと思いませんか。
たとえ学校に行かなくても、どんな状況でも勉強はできるし、研究はできるんですよね。
それはあなたが炎が不思議だと思ったのと同じように、何かが不思議だなぁ、そのからくりがわかったらおもしろいなぁ、という気持ちを持ち続けることができさえすればできることなんだということを教えてくれます。
※この本(原題 Chemical History of A Candle)は,三石巌さんの訳が,角川文庫(ISBN: 4043127014)から出ています。
また絶版になっているようですが、矢島祐利さんの訳が岩波文庫(青909-1)から、吉田光邦さんの訳が講談社文庫(ふ 23-1)からも出ています。
図書館か書店で探してみるとよいでしょう。なお,山形浩生さんの訳を以下のURLで読む事ができます(ただし,実験装置の挿絵は載っていません)。「あとがき」が出色です。
http://www.genpaku.org/candle01/candlej0.html
上記サイト「プロジェクト杉田玄白」は、著作権の切れた洋書などの翻訳を無料で公開しています。「ロウソクの科学」以外にも、優れた古典的作品が多数収録されています。
化学結合が強ければ体積弾性率は小さくなるのでしょうか(つまり固体AよりBの体積弾性率が小さいのでAの構成原子間の結合がBより弱いと言えるか)?
また結合の強さは明白に共有結合>イオン結合>金属結合>ファンデアワールス結合となるのでしょうか?
それともあるイオン結合はある共有結合より強いということが起こりえますか?
固体の力学的性質をミクロな視点から解明して行くことは基礎物性だけでなく応用上も非常に重要な研究分野のひとつです。
しかし、そのような性質をミクロな視点から一概に議論することはそれほど簡単ではありません。
さて、等方的な物体を液体中に置いて静水圧をかけると物体は外形を保ったまま小さくなります。
その際の圧力に対する体積変化率として圧縮率、またその逆数である体積弾性率を測定することができます。
もし、原子間の結合角が全く変化しない物質 を想定して圧縮を議論する場合は、体積弾性率に効いてくるのは距離の変化に対するエネルギーの変化率です。
つまり原子間の平衡距離からの微小変化ΔRに対するポテンシャルエネルギーの変化を [k(ΔR)^2]/2 と近似すると、原子の熱運動を無視すればkの大きさで体積弾性率は決まります。
kは平衡位置でのバネ定数と考えることができます。しかし、原子間の平衡距離は斥力と引力がバランスを取った状態で決まりますので、バネ定数は結合の強さそのものではありません。
たとえばファンデァワールス力で凝集したものとして、アルゴンの固体を例に取ると原子間の結合は非常に弱いにもかかわらず、圧縮率は氷と同程度でそれほど小さくありません。
これは閉殻状態の電子はパウリの原理により他の電子の進入を排除 しますので、力を加えて閉殻電子配置を変形させるにかなり大きなエネルギーを必要とします。
そのため、原子同士が近づくとある距離から急激に斥力が増大します。
これらの様子を再現する関数形としてレナード-ジョーンズポテンシャルが良く用いられます。またイオン結合でできているNaCl 結晶を考えてみると、Na原子は電子 をひとつ失ってNeと同様の閉殻電子配置になります。
一方、Clは電子をひとつ得てAr と同様の閉殻電子配置になります。電荷をもつイオン間の相互作用は長距離力ですので、正負のイオン間の引力だけでなく、正イオン同士、負イオン同士の斥力も考えますが、それだけでは平衡距離は説明できません。
アルゴンと同様に、ある距離より近 づくと閉殻の電子配置のイオン間の斥力が急激に大きくなります。
正負のイオン間は 引力ですので互いに接近していますが、その状態で更に圧力を加えるわけですので、比較的大きな体積弾性率を示します。
このとき引力としてはファンデァワールス力も作用していますが、他の相互作用よりもかなり小さいのでほぼ無視していても良いわけです。
同じイオン結晶でもイオンサイズの小さいLiFではイオン間の距離も小さく、NaClの倍以上の体積弾性率を示します。
一方、代表的な共有結合性の結晶である SiではNaClの数倍の体積弾性率、ダイヤモンドでは数十倍の体積弾性率を示します。
これはシリコンや炭素原子間の共有結合においては、結合距離を変化させるのに非常 に大きな力が必要であることを示しています。
しかし共有結合では結合角も決まっていて、SiやCでは正四面体構造をとります。したがって、これらの物質ではより密 に原子を配置する最密充填構造(例えば六方最密構造や面心立法構造)ではなく、比較的すき間の多いダイヤモンド構造をとるのはそのせいです。
一方、金属結合の代表 的な物質であるアルカリ金属は電子の海の中にアルカリイオンが浮いているというイメージが近いのですが、電子の海を外から圧縮するためその体積弾性率は小さく なり、固体アルゴンと同程度の値になります。
なお、ここでは圧力を加えたときにその構造が変化しない範囲で考えているわけですが、更に高い圧力を加えると一般に 結晶構造も変化します。
これらの典型的な結合様式をもつ物質では、ある程度類型的に比較することができますが、多くの物質はそれほど簡単ではありません。
その理由は色々あります。ひとつ は、例えば半導体結晶として良く用いられる GaAs(閃亜鉛鉱構造 zincblende structure)などの化合物半導体では、共有結合とイオン結合が混在しています。より イオン結合性が強くなると、CdS のようにウルツ鉱構造 wurtzite structure に変化 します。
つまり、単純に何々結合と分類することはできません。遷移金属も同様で、 金属結合と共有結合が混ざっています。
もうひとつの例として、分子性結晶のように分子内は共有結合性が強くても、分子間の結合は非常に小さくて圧力を加えた際の構造的な変形が均一ではありません。
種類の異なる結合が固体中に存在している わけです。さらに、加圧によって結合距離ではなく結合角が変化する場合です。たとえば、C60が並んだ固体を想像してみると良いでしょう。
この他に、力学的性質としては体積弾性率だけでなく変形などの性質も重要で、固体では応力とそれによる変形との関係はテンソルで与えられます。
また金属のように展性や延性をもつのは、原子面の滑りが起こっても同じ結合を再現できるため構造的に壊れにくくなります。
逆に共有結合性が強い半導体やセラミックは原子面の滑りは起こりにくく、限度を超えると壊れてしまいもろくなります。
一般に引っ張り強度も低くなります。また、高分子材料や性質の異なるものを複合したハイブリッド材料もあり、それぞれ特徴があります。
結合の強さについてですが、ファンデァワールス力に相当する成分は常に存在しますが、一般に他の相互作用よりも弱くなっています。
イオン結合は原子サイズが小さくなると顕著になりますが、一般には典型的な共有結合物質よりは弱いと考えられます。
純粋な金属結合はあまり強い結合ではありませんが、多くの金属は金属結合以外 の結合が混成しています。
あまり用語に縛られないで、多様な構造をもつ固体において電子の示す多彩な性質のひとつとして広く考えられると良いでしょう。
Is glass, in liquid form, a conductor of electricity? (Middle School Teachter)
"Glass" is a term used to specify, in the widest sense, a thermodynamically non-equilibrium state where any disorder is frozen in. The most familiar example of glass is amorphous (or vitreous) solid as often seen as window-glass. The term "glass" is used for this type of glass in the narrowest sense. This type of glass is usually prepared by quenching liquid (resulting in "glassy liquid"), and consequently, has essentially the same structural features. This is why the window glass is often said to be a kind of liquid. Other types of glass also exist. Glassy liquid-crystal is formed by quenching liquid crystals, where orientational order of molecular arrangement exist while translational one does not. Some glassy crystals are formed by quenching orientationally disordered (but positionally ordered) crystals. Spin glass is also glass where disordered spin arrangement is frozen-in, in contrast to previous examples having frozen-in structural disorder.
According to the above interpretation, the term "glass" is not directly correlated with conducting property of matter: Some glasses are conducting whereas others are not. Amorphous metal is electronic conductor. Most amorphous (inorganic) salt will be insulating because ions are effectively immobile in this frozen-in state, though molten salt is surely conducting (electrolyte or ionic conductor). There are however some examples of amorphous salts showing ion conduction. In such cases, small ion(s) run(s) through free volume formed upon glassification (most glass has larger volume than crystalline states). For non-electrolyte and nonmetallic melt, there is no reason to suspect that their quenched glasses are conducting. If your question intended to ask whether is the "melted" glass (in the narrowest sense) conducting, the answer is "no". The glass is mixture of oxides (main component is SiO2), which are insulating.
私は化学科で、環境問題(特に地球温暖化)について学びたいと思っています。
私の学校では、2年進級時に物理・生物の選択を行うのですが、私は生物を選択しました。
けれど大学の授業では物理もカリキュラムに入っているようで、中学までの物理の知識しかない私にはついていくのが難しいでしょうか?(高校2年生)
大学で化学を学ぶには物理の基礎的な知識は必ず必要になります。
それゆえ、高校で物理を履修しておく方が望ましいのは言うまでもありません。
しかし現状では、化学科入学者の1/3程度の学生は生物を選択してきています。
そのため大学の物理の授業について行けず、落ちこぼれる学生がかなり出る問題が生じました。
その対策として、物理未履修者を対象とした授業を最近開講しました。
最終的なゴ ールは同じですので、学習する意欲さえあればきっと大丈夫です。
環境問題に化学からアプローチしたいというあなたの考えは非常に結構だと思います。頑張って下さい。
A cement compound CaO.Al2O3.10H2O gives certain peaks when using the powder diffraction method. The compound now increases its water of cystallization to become CaO.Al2O3.11H2O. Will the diffraction pattern obtained be basically the same as the former, with only a slight difference which corresponds to a slight increase in the d-spacing? Or will the diffraction pattern be an entirely different pattern?
Generally, a chemical formula is insufficient to identify the chemical. For example, C is used for diamond and graphite, and even for buckminsterfullerene (C60), all of which are allotropes of carbon. Their diffraction patterns are, needless to say, entirely different. We must identify the crystal form or phase to discuss the structure and physical properties. There are however some crystalline compounds of which the composition continuously changes. They are called non stoichiometric compounds or berthollides after a French chemist C.L. Berthollet. Many proteins require some water molecules to be involved in crystal, and the content of water can vary depending on the external condition. For non-stoichiometric compounds, the diffraction pattern remains essentially the same in some composition range. As for materials you consider, we find the information only for CaO.Al2O3.10H2O, which was reported by Carlson in J. Res. Natl. Bur. Stand. (U.S.), 59, 107, 1957. You should consult some database by yourself at libraries of your convenience for further search as our search may be incomplete. If you made the experiments on CaO.Al2O3.11H2O, the following should be remembered: The similar powder diffraction pattern to CaO.Al2O3.10H2O is definitely insufficient to claim that CaO.Al2O3.11H2O is non-stoichiometric. The sample showing the composition CaO.Al2O3.11H2O may be mixture.
化学を学んで、研究者になるにはどのようなことが必要でしょうか。
化学に限りませんが、まず大事なのは、「 好奇心」と「 探求心」です。好奇心を持ち理由を明らかにしようとする探求心は研究の大きな原動力です。また、勉強と研究に対する継続的な努力、新しいことに挑戦する勇気、そして、研究は常にうまく行くとは限りませんから、問題解決のためには柔軟性と忍耐力も必要となります。化学の研究では実験が大きなウェイトを占めますので、実験好きの学生さんを歓迎しますが、実験が苦手でも化学をやりたい人は、理論や計算機化学を専門とする研究室に入るといいでしょう。小さなことでも目的を達成するとうれしいもので、それによって自信と新たな興味が生まれ、新しい研究の原動力になります。
“化学”という名の付いた学科は、大阪大学には理学部以外に工学部、基礎工学部や薬学部にもありますが、いったいどこが違うのでしょうか。
当然疑問に思われる点だと思います。それぞれ特徴を持っていますが、お互いの研究領域が一部重なり合っている部分もあり、はっきりとした境界線を引けない面もあります。しかし、一般的には、理学部では化学の広い分野にわたって主として基礎的・学術的研究を行っているのに対し、他の学部ではそれぞれの目的に添った化学の限られた分野での応用的研究に重点があります。ご存じのように、日本の科学技術はたいへん進んできましたが、基礎科学の分野でももっと世界に貢献することが求められており、理学部の役割もますます大きくなっています。“理学”の基本は“なぜ?”という好奇心です。これに答えるにはしっかりとした基礎学力と柔軟な思考が必要です。実力を充分養った理学部の卒業生は応用力にも優れているので、社会的にたいへん高い評価を受けています。
環境問題に関心があるのですが化学科で勉強できますか。
環境問題のほとんどが化学に関わっていますし、実際に各分野で環境問題に取り組んでいる卒業生も多くいます。将来その分野で貢献するためには、なるべく広い視野で基礎をしっかり勉強することが必要になります。当化学科には、「 環境」を冠した講義や研究室こそありませんが、カリキュラムの内容は充分それに対応しており、広い意味で環境に関わる研究も多く行われています。
化学科卒業生の進路、就職状況はどうなんでしょうか。
学部卒業生の8~9割の人は大学院に進学し、1~2割の人が就職しています。大学院では、多くの人が修士課程修了後に企業に就職していますが、さらにその2~3割の人が博士課程に進んでいます。博士課程を修了して学位を取ると、主に大学や国立の研究機関に就職し、第一線の化学者として活躍しています。最近では企業の研究所に就職する人も増えています。進路、就職状況をこちらにまとめてありますが、化学科には、毎年平均して400件に及ぶ求人があります。やはり化学系企業への就職が最も多いですが、最近は電気・情報など他の分野への進出も増えており、卒業生は多方面で活躍しています。
入学前に大学を見学できる機会はありますか。
もちろん何回かのチャンスがあります。基本的には、春の「いちょう祭」(5月初め)と秋の「まちかね祭」( 11月初め)の時に大学内公開になりますし、8月には大学説明会があります。大学祭中は多くの研究施設などの公開がされており、化学科でもいくつかの研究・教育施設や研究室の紹介や公開をしています。今年の「 いちょう祭」では研究室の紹介ツアーを企画しましたが、高校生も多く参加し好評だったようです。また、各種のアウトリーチ活動も開催しています。これにも多くの高校生が参加し、最先端の研究施設の見学や実際にいろいろな実験をすることで大学生活の一端を経験しています。
生物学について
単細胞生物は一般に無限増殖を繰り返すので、事故がなければいつまでも死なないが、我々ヒトはいつか死にます。
単細胞生物が不死で、ヒトがなぜ不死ではないのかを、アポトーシスの観点から教えてください
難しい質問ですね。実験して答えを出すことができないことなので、「一つの考え方にすぎないが・・・」とお断りしておきます。
「単細胞生物は一般に無限増殖を繰り返す」わけではありません。
池の水の中などに住んでいる単細胞生物、原生動物は、 遺伝子交換=有性生殖(接合)をしないかぎり、有限回で増殖がとまります。
今からちょうど50年前の1954年、米国のソネボーンという研究者がゾウリムシの1匹が分裂して2匹になったら、それぞれ分けて1匹ずつ別の容器に入れ、 その次分裂したらまた分けて、と繰り返して絶対に接合しないようにしてやったところ、 約350回分裂したところでそれ以上分裂しなくなり、 やがて死にました (当時、アポトーシスかネクローシスか、という考え方はありませんでしたが、 今見直すとアポトーシス的です)。
つまり単細胞生物にも寿命はあるのです。
いいかたを変えると1匹のゾウリムシから出発した「姉妹細胞の集団」を一まとまりに考えると、有性生殖をしないかぎり寿命が来て死にます。
さて、次に「多細胞生物である我々ヒトはいつか死ぬ」かどうかを考えてみましょう。
個体としては確かにそうですが、遺伝子からみたらどうでしょう。
ヒトは、生殖細胞(卵か精子)に遺伝子を伝え、 生殖細胞は別の個体由来の生殖細胞と接合できれば受精卵となり、分裂して新しい個体を作ります。
その個体は、その中でまた生殖細胞を作って次代に遺伝子を伝えます。 つまり遺伝子は無限に受け継がれます。遺伝子としては「死んでいない」のです。
この二つの話を並べてみてどう思いますか。 もし「1匹のゾウリムシから増えた姉妹細胞集団」と「多細胞生物であるヒト1個体」とを同じ位置に置くと、 そっくりでしょう。有性生殖をしないかぎり、遺伝子の等質な細胞集団には寿命が来るのです。
しかし、有性生殖がなされれば分裂回数カウンターがリセットされ遺伝子としては寿命はありません。
ただ違うのは、ゾウリムシは姉妹細胞が分かれてそれぞれ勝手に泳いでいるけれど、 ヒトは1個の細胞(受精卵)から増えた姉妹細胞が分かれないで団体行動をしている、というだけの違いです。
高校で生物を選択せずに大阪大学の生物科学科に入りたいのですが、大学の勉強にはついていけますか?
大阪大学理学部生物科学科の新入生のうち、約半数は受験科目に生物を選択していません。
その中には、高校で一応習いはしたが受験に使わなかったという人が約半数いますが、 まったく習わなかったという人も約半数(結局全体の約四分の一)います。
そのため、高校で生物を履修しなかった学生向けの「補習」的な集中講義が 1年生の4・5月に用意されています(医・歯・薬学部学生と合同)。
これを受講することで、かなりの程度追いつくことができます。しかし、精力的な自習が不可欠なことも事実です。
理学部のバイオと農学部のバイオの違いを教えて下さい
研究者の日々の作業は同じです。医学部とも薬学部とも工学部とも同じです。違うのは何を目指してその作業をしているのか、という点です。
ミッションが違うという言い方をしてもいいでしょう。
たとえば、農学部でイネの遺伝子の研究をしている人がいます。
それは、お米の収穫 を上げるためとか、寒い地方で育つイネを作り出すためとか、乾燥に強い品種を作ろうとか、農業生産利用の目的があってやっている場合がほとんどです。
理学部生物にも、イネの遺伝子の研究をしている人がいます。しかし、たぶんその人は生産に役立てようと思っているわけではなく、植物の受精の仕組みを知るためだったり、植物と動物の遺伝子の制御様式の違いを知るためだったりします。
それらを調べるのには、 品種の系統がしっかり記載されているイネは野生のタンポポより好都合だから、イネを実験対象に選んでいるのでしょう。
このように、理学部の生物研究は産業に応用するために行っているのではなく、自然の仕組みを知るため、ちょっと大げさにい うと人類の叡智を増進するため、に行っているのです(結果的に産業に応用できることもありますから、そうなったら一層嬉しいでしょうけれどそれが第一目的ではありません)。
同じように、医学部でネズミの胃酸分泌の研究をしている人は、胃潰瘍の原因解明や治療に役立てようと思って行っているのでしょうが、理学部でネズミの胃酸分泌の研究をしている人は、細胞がH+イオンをどうやって輸送するのか、ひいては細胞はどうやって物質を出し入れするのか、その仕組みの根本を知りたいから行っているのです 。
したがって、研究の具体的内容はほとんど変わりません。
現実に、理学部出身者が医学部の基礎医学部門の先生になることは珍しくない(どころか、ごく普通のこと) ですし、食品会社や薬品会社に就職して農学部出身者や薬学部出身者と机を並べて仕事をしていることも、ごくごく普通のことです。研究成果を発表する学会も共通です。
ただ、上の目的の違いを反映して農学部だと研究材料が食用植物だったり、森林昆虫だったり、養殖魚だったり、家畜だったりすることが比較的多く、医学部だと哺乳動物や、病原微生物だったりすることが比較的多いのに対し、理学部だととくにそのようなことはなく、普段なじみのない生物を相手にしている人も少なくない、といった違いは出てきます。
一度、お近くの大学の学園祭やオープンキャンパスに出かけて、研究室を案内してもらったり、そこで研究している学生や大学院生と話をしてみることをお奨めします。
共通点と相違点を実感できると思います。そしてどちらが自分にフィットするか、感覚がつかめると思います。
顕微鏡を使って小さなミクロの世界を探究したいなと漠然と安易に考えているため、具体的に微生物を学んで、何をどうしたいんだという問いに明確に答えることができません。
他の生徒の目的意識がどのようなものか知りたい。
探究したい考えはそれで大変結構なことだと思いますが、そうやって研究することは必ずしも微生物だけのことではなくて、全ての「生きている」ものの研究には、そのような「顕微鏡を使って小さなミクロの世界を探究」する部分が含まれています。それがなければ全体像を解きあかすことが出来ないくらい大事なことですので大事にしていただきたい。
その部分で他の方との意識の差がそれ程あるとは思いません。
生物分野における他大学との特色の違い、とくに、京大、神戸との偏差値以外の違いがよくわかりません。
また募集人数が少ないのはどうしてですか?
京大との違いは特にないと思いますが、神戸との差はその規模が少し違うかなというくらいで、研究・教育内容がそれ程違うとは考えにくいと思います。
募集人数は、かってどこの大学も同じような規模でしたが、大学が大きくなる段階で他大学は生物学科を大きくしました。
阪大は必ずしもその潮流には乗らず、少数精鋭で行くと決めたのだと思います。
今でこそ生物を志向する人たちは多いですが、将来ははたしでどうでしょうか。誰にも分からないところです。
生物科学科の定員が少ないことによるデメリット、例えば窓際的な存在となり、研究費、人材が回ってこないことや、閉鎖的な環境になっていること、があるのかどうか現場の様子が知りたいです。
もちろんメリットも魅力的なので知りたいです。
他大学との比較で気にさわるかもしれませんが、正直に書くと、京大理学部生物科学専攻、農学部応用生命科学科、阪大理学部生物科学科の3つの選択肢で迷っています。
仮に、これらすべてが合格圏内として偏差値を抜きにして考えた時の阪大生物科学科の魅力、つまり京大にはない魅力とは何ですか?
デメリットということを特に想像することは難しいですね。
むしろ、そこにいる人 にはメリットの方が多いと思います。窓際に行く暇がありません。
また情報の伝達を円滑にし、閉鎖的な環境にならないような積極的な運営を心掛けています。
上に述べたように、まず少数精鋭で基礎的な生物学教育を受け(学生一人に先生2人)、その後大学院理学研究科はもちろん、理学研究科と協力関係にあって阪大に付置されている多くの生物学関係の研究所(蛋白質研究所、微生物病研究所、産業科学 研究所など)を含めて将来を展望することが可能である、という点ではないでしょうか。当然、それ以外の医学部、歯学部、薬学部などの大学院研究科にも道は開かれていますので、そちらに向かうことも可能で実際多くの学生の選択肢にもなっています。
動物の行動学を学びたいと考えていますが(環境問題にも興味があります)、貴校ではそのような研究について学ぶことができるのでしょうか?
他の大学の農学部との間で悩んでおります。
動物の行動学は、1)その行動は生まれながらに備わっているものか、生まれてから備わる可塑的なものか(発達)、2)行動の神経やホルモンのメカニズムはどうなっているか(しくみ)、3)行動がどうやって進化してきたか(進化)、4)その行動はどれだけ遺伝子を残すのに有利か(適応)という4つにわけて研究されています。もちろん、動物行動に興味を持つ研究者はこれら4つすべてを自ら解き明かしたいのですが、なかなかそうもいきません。研究者によって中心を置く位置が異なります。あなたは行動学のどの分野に特に興味をもっていますか?私たちの専攻では、2)の神経行動学に関連した研究室がありますので、行動のしくみを中心に1)発達や3)進化の観点で行動学を学ぶことができます。もし、あなたの興味が4)の適応であるなら、行動生態学という分野を探してみて下さい。現在のところ当専攻には行動生態学を専門としている研究室はありません。また、理学部と農学部の行動学研究の違いとして、農学部は昆虫(益虫、害虫)や哺乳類(家畜)を対象とした行動学研究を中心とすることに対し、理学部はそれらを含めたより多様な動物を視野に入れていることが挙げられるでしょう。
大学で食品の栄養素など天然高分子の研究をしたいと考えています。大阪大学の理学部では生物科学と化学のどちらの学科がいいのでしょうか。
もし化学科だとしたら、化学科では物理が重要と聞きますが、受験で生物を選択した私でもついていけるのでしょうか。
現在、化学と生物学の境界はかなりぼやけてきており化学者と生物学者の両方が同じ分野を研究することも多くなってきています。
研究したいと考えている食品の栄養素や天然高分子は、まさにそのような境界領域の分野だと思います。
あえて違いを挙げるならば、栄養素や天然高分子そのものの性質や化学変化について調べるのが化学、 栄養素や天然高分子によって人体がどのように応答するかを調べるのが生物学だと言えるかも知れません。
ただし栄養素や天然高分子が人体に与える影響を追求していくと、それらの化学的性質をよく理解しておくことが必要でそれには化学の知識が不可欠になります。
化学を習得するには、物理の素養も必要ですが現在化学科に入学してくる学生さん の約1/3は、高校のときに物理を選択していません。
入学後は物理の講義もとる必要がありますが、高校で物理を選択していない学生さん向けの物理の授業を開講していますのでそこで高校で習っていなかった分を補うことができるようなカリキュラムになっています。
理学部は工学部などに比べて就職が厳しいと聞きましたが、大学院まで進んだ場合はどうなのでしょうか?
よく「理学部や理学研究科は就職”無理”学部」などと言われているようですが、断じてそんなことはありません。
大阪大学理学部および理学研究科では、数学・物理学・化学・生物科学の幅広い知識はもちろんのこと、複雑な自然現象を司る原理・原則、さらにそれを基盤とした論理的思考についてしっかりと学んだ上で、世界の最先端の研究を行っています。
企業でも新しい技術や製品の開発をする際には、複雑な事象の中から本質的な問題を抽出し解決する能力が求められます。企業への就職先については、工学部のように特定の業種に限定することはありませんが、理学部/理学研究科の卒業生は幅広い素養をもつ人材として多方面から期待されており、毎年たくさんの求人が全国の企業や国の機関、高等学校などから届き、巣立って行きます。
大阪大学では、理学部の卒業生の2~3割程度が企業や高等学校教諭などに就職し、残りの7~8割程度が大学院の博士前期課程(修士課程)に進学しています。
大学院博士前期課程の修了者(修士)の7割程度が企業や高等学校教諭や国家公務員などに就職し、1~2割程度が大学院の博士後期課程に進学しています。
博士後期課程で博士(理学)の学位を取得した方は、大学教員や研究所の研究員や企業の研究開発スタッフとして活躍しています。
生物科学科と医学部では発癌制御の研究の違いはありますか?
具体的には同じです。
ですが、発想(あるいは目的意識というか使命というか)が違います。
医学部での研究は、最終的には医療に役立てるためですから、それを意識した問題設定をします。かといって、ヒトや哺乳動物の細胞しか扱わないかというとそんなことはありません。ガンは細胞増殖の異常ですから、すべての生物に共通な「細胞分裂の制御機構」と密接に関連しています。
だから、医学部でカエルの受精卵の分割を研究している人もいますし、酵母菌の分裂の仕組みを研究している人もいます。
もし、細胞分裂のある特定の場面で植物細胞の方が実験に好都合であれば、植物を使っている人がいてもおかしくありません。
そこで得られた発見や知識をヒトのガン細胞に試してみてうまく行けば大成功ですから。
でも、うまく当てはまらないかもしれません。医学の研究だと当てはまらなければ「残念、失敗」です。
でも理学の研究なら失敗ではありません。次の問いが出てきます。なんでこの場面ではヒトと植物と違うんだろう、何が同じでどこが違うんだろう、と。
それを掘り下げれば、一段深い理解ができるかもしれません。それは理学の研究の目的が、必ずしも医学や薬学や産業に役立つことではなく(役に立ったらもちろん嬉しいですが)、自然界の原理を解明して人類の英知に寄与すること(ちょっと大げさかな)だからです。
したがって、日々行っている具体的な実験内容という意味では全く同じですし、現実に理学部の出身者が医学部の基礎医学の研究室(実際に患者さんを診る臨床部門ではなく、解剖学、生理学や病理学などの研究部門)にはたくさんいます。むしろ医学部出身者より多いくらいです。違うのは、その具体的研究の先にある目標です。
生物学に進みたいと考えていますが、将来の展望がひらけているのはどういう分野なのでしょうか?
「将来の展望」が確実に予測できれば、現在の日本の不景気もなかったし、私も ○ー○○賞がとれていたはずですで、それはわかりません。
変化の早い生物学ではとくにわかりません。DNAの二重らせん構造が提唱されたのが今からちょうど50年前で、 そのとき50年後のバイオ技術の隆盛を予測できた人は、世界中に一人もいなかったと思います。
でもそういったら何もいえなくなってしまうので、以下は「確実にそう なるかどうかわからないが」という但し書き付きでの予想です。外れたらごめんなさい。
まず、産業的な応用面では、バイオ育種がもっと広がるでしょう。今は、遺伝子組 み替え作物に対する漠然とした不安があって、先進国には忌避傾向がありますが、世 界レベルでの人口爆発に対応するには、そんなことはいっておられず、中進国で日常 技術化するでしょう。そして問題ないという証拠が積み上がれば、先進国に逆流して くるでしょう。食べる作物ではなく、砂漠緑化技術の一環としてのバイオ育種もあり えます。地球温暖化を食い止めるため、炭酸ガスの再固定を高める必要があります。 乾燥に強く成長の早い植物の作出に期待がかかります。同時に炭酸ガスの排出を減ら すには、代替エネルギー開発とならんでゴミになったら燃やさなくてはならないプラ スチックに代わる生分解性プラスチック(カニの殻利用とか)の開発も必要でしょ う。クローン牛や豚を作る生殖技術は、すでに実用化可能かどうかの検討段階は終わ り、今は産業化の段階に入っています。
医療面では、テーラーメード医療(患者個人個人の体質に合わせた医療)の基礎と なる遺伝子多型分析技術は、今は病院内技術ですが、いずれ健康産業にアウトソーシ ングされるでしょう。医薬そのものも、今のような有機化合物から抗体とか結合ペプ チドのような、生体により馴染む物質に置き換えられていくでしょうから、そういっ た産業の需要が高まるでしょう。移植医療との関連で、臓器を作り出す発生工学技術 も10年後くらいには産業化のメドがつく可能性があります。
実は、上のような産業上のことは、現在行われている基礎研究がそういう方向を志 向していることから、10-20年先をある程度予測可能です。しかし、基礎研究が10-20 年先何をやっているかは、ほとんど予測不可能です。今から20年くらい前、あるアン ケートで「20年後の基礎生物学研究の主流は」と訊かれて、「ズバリ、宇宙移住のた めの生物学や冬眠の科学」と回答した覚えがあるのですが、正解ではなかったようで す(でも、あと10年したら、やはり正解になるかもしれません)。強いて挙げれば、 長寿化社会を迎えて痴呆予防・治療の基礎となる脳科学。高ストレス社会のせいか環 境毒物のせいか不明ながらじわじわと増加傾向にある精神疾患の科学。新手の感染症 もきっと登場するでしょうから、そういった微生物の科学。ガンの基礎研究(今は少 し下火になっているのですが、病気としてのガンは全然減っていないので、何かの突 破口があれば、ふたたび隆盛を取り戻す可能性あり)。上に書いた生殖工学や発生工 学(基礎研究としては、今よりもう一段深化して)。でも、このあたりは、誰でも挙 げるところでしょうね。誰も予測できないことを予測すると、・・・。できるわけな いじゃないですか。
なお、少し違った見方では、先端技術が市民の常識とは離れてしまうことからくる 社会の不安を埋めるため、生物学に知識と見識のあるジャーナリストの需要が高まる はずです。欧米の先進国ではそうですから、日本もそうなるでしょう。
科学・理学部一般について
他学部からの転部や理学部の大学院への進学は可能でしょうか?
他学部学生に対する理学部への転部選考試験は、毎年10月上旬に学内掲示板でお知らせします。
また大阪大学の他学部を卒業し、理学研究科博士前期課程へ進学する事も可能です。
理学研究科博士前期課程の大学院入試を受験してください。
詳しくは、こちらをご覧ください。
文系の大学を卒業して今27歳になります。どうしても一生研究を続けていけるような研究者、技術者になりたいと思い、理学部や工学部の再受験を考えています。来年合格したとして学部卒業が32、修士卒業が34になります。
研究者としての就職口はあるでしょうか?
研究職に就いている人の多くは、程度の差こそあれ、かなり高い年齢になってから「定職」に就いています。
特に最近では「一生研究の出来る定職」に就く前に、「ポスドク」と言われる期限付き雇用期間(武者修行のような期間)を経ることが多くなっています。30歳代半ばで、ようやく「定職」に就く例も珍しくありません。
ですので、年齢に関しては一般企業に比べるとシビアな問題ではないようです。
しかし、修士を修了しただけで「一生研究を続けることの出来る」ポストに就くことは、(年齢に関係なく)まず無理でしょう。博士の学位も必要です。
となると、さらに3年以上かかります。それでも研究能力が高ければ、就職先は必ず見つかるはずです。
要するに年齢よりも能力で判断されます。貴君に「やる気」と「能力」さえあれば、道は開けると思います。
かといって、(貴君に対してだけでなく誰に対しても)「《絶対に》就職口はある」とは断言できません。
転学部について、試験の有無、受験資格、日程、大学受験時の成績のことなど、できるだけ詳しく教えて頂けませんでしょうか?
他学部学生に対する理学部への転部選考試験は、毎年10月上旬に学内掲示板でお知らせします。
受験資格は大阪大学の学部学生である事ですが、願書提出の事前に転部希望先学科の学科長とお話ししていただき、願書に学科長の承認印をいただいてもらっています。
ただし、大学入学共通テスト(旧:大学入試センター試験)および2次試験の成績によっては出願しても受験できない場合があります。
現在、他大学の一年で理学部物理学科に進んでいますが、3年次に大阪大学へ編入を考えています。
他大学からの編入という人は多いですか?
また、一般に大学受験と3年次編入と大学院試験ではどれが入りづらいのでしょうか?
理学部では高専を含めた他大学からの編入は行っていません。大学院修士課程からの入学をお勧めします。
理学部は工学部などに比べて就職が厳しいと聞きましたが、大学院まで進んだ場合はどうなのでしょうか?
よく「理学部や理学研究科は就職”無理”学部」などと言われているようですが、断じてそんなことはありません。
大阪大学理学部および理学研究科では、数学・物理学・化学・生物科学の幅広い知識はもちろんのこと、複雑な自然現象を司る原理・原則、さらにそれを基盤とした論理的思考についてしっかりと学んだ上で、世界の最先端の研究を行っています。
企業でも新しい技術や製品の開発をする際には、複雑な事象の中から本質的な問題を抽出し解決する能力が求められます。企業への就職先については、工学部のように特定の業種に限定することはありませんが、理学部/理学研究科の卒業生は幅広い素養をもつ人材として多方面から期待されており、毎年たくさんの求人が全国の企業や国の機関、高等学校などから届き、巣立って行きます。
大阪大学では、理学部の卒業生の2~3割程度が企業や高等学校教諭などに就職し、残りの7~8割程度が大学院の博士前期課程(修士課程)に進学しています。
大学院博士前期課程の修了者(修士)の7割程度が企業や高等学校教諭や国家公務員などに就職し、1~2割程度が大学院の博士後期課程に進学しています。
博士後期課程で博士(理学)の学位を取得した方は、大学教員や研究所の研究員や企業の研究開発スタッフとして活躍しています。
阪大の学生や教授は他大学に比べて真面目だと聞きましたが、本当なのですか?
《学生、特に理学部・理学研究科の学生について》
阪大の学生(学部と大学院があります)は、もちろんとても「真面目」です!
多くの学生は講義や実験やセミナーにきちんと出席しています。4年生になって研究室に配属され、さらに大学院に進学すると最先端の研究に従事しますが、日夜そのための努力を惜しみません。
特に最先端の研究のためには、与えられたことをこなすだけの真面目さではもの足りません。自分から積極的に関わってゆく「真剣さ」がとても大切です。
苦労もありますが、成果が得られたときの充実感や達成感には計り知れないものがあります。
このように高度な専門的知識を得たりその経験をして立派に卒業した後には、それを仕事に生かすことが待っています。
大阪大学を卒業した人たちは、企業や大学などで活躍し指導的立場に立つ方も大勢います。
大切なことは、外部から押しつけられた「真面目」ではなくて、阪大学生自身の内部から自発的に生まれ出てきた「真面目」だという点です。
《教授について》
阪大の教員は真面目か。
確かにそうかもしれません。なぜだか、分析してみましょう。
一つには、理系学部が多いことによります。阪大はもともと医・理の2学部で出発した大学です。
現在は法学部も経済学部も文学部もある総合大学ですけれど、学生比率も教員比率もやはり理系に重心がかかっています。
ではなぜ理系が多いと「真面目」か。
理系は論理が柱です。個人の性格の上ではいい加減な教員もいっぱいいますが(かくいう私も、その点では人後に落ちませんが)、仕事の上では論理を貫かなくてはなりません。
1+1は3だといったら、芸術なら独創的とほめられますが、科学ではバカといわれます。
誰がやっても2です。クソマジメでつまらないといわれても、これを崩すわけにはいきません。
また、理系は知識の積み重ねが必要です。個人の才能だけではどうにもならないところがあります。
伝達すべき情報は増える一方なのに、休日は増えるし土曜日は休みだし、授業時間が足りません。いきおい、休講はありえず授業は定刻に始まり、終わりは定刻を超えることも少なくない。これを外からみればキマジメとしかいいようがありません。
さらに、理系教育は実験が重要です。実験・実習には、材料や器具・機械の準備が必要です。ふらっと来て、気ままに実験して飽きたら帰る、なんてことはできません(文系はそうだという意味ではないけれど、教育システムとしては、文系よりはるかにスケジュール重視になります)。
したがって、その点からも休講なんてありえません。同じことともいえますが、理系の研究は紙と鉛筆があれば十分、ということは稀で、技術が必要です。
その技術の伝授には現場指導が不可欠です。だから高学年や大学院では少人数指導になり、そうなると教員は(学生も)連帯感が強まってサボらなく(サボれなく)なります。
もう一つの、意外に大きな理由は立地条件です。盛り場から遠く、誘惑が少ない。
東大なら駒場キャンパスは渋谷の隣だし、本郷キャンパスは池袋にも銀座にも近い。京大、北大は京都、札幌の町の中心にあります。
昔は阪大も大阪都心にあったのですが、今は郊外です。飲みに出ようがない。
それでも豊中キャンパスには阪急石橋阪大前駅周辺の商店街があるけれど、吹田キャンパスの隣りは万博記念公園ですから、夜になったらフクロウとタヌキしかいません。
駅から遠いと車で通勤することになり、飲めない。教員は(学生も)好むと好まざるとにかかわらず、研究に没頭できるわけです。
それで、かどうかわかりませんが、多くの研究室では折りに触れ、ゼミ旅行や新人歓迎お花見や卒業生歓送行事を企画して日頃の飲み足りなさを取り返します。
統計がないのでわかりませんけれど、ゼミ行事率なら阪大はトップクラスではないでしょうか。
というわけで、結論。阪大の教員は、心底真面目かどうかは大いに疑わしいけれど、少なくとも「見かけ上は」確かに真面目です。
僕は高校1年生で、高校の数学にとても魅力を感じ楽しく取り組んでいます。
ですからそれを発展させた数学を学べる数学科に行こうと思っています。
しかし数学というのは既に研究され尽くした学問だと最近感じるようになってきました。
そう考えると意欲がそがれる気分になってしまいます。まだ数学には未開の分野はあるのでしょうか?
今から100年近く前に、ポアンカレが次のような講演をしています。
「かつて数学の未来は不幸であるとの予言があった。
これらの予言者は全ての問題は解けてしまって、未来は落ち穂を拾うことしか許されていない、と言った。
しかし、これらの悲観論者はいつも退却せねばならなかった。
今日は、こういう悲観論者はいないと私は信ずる。」
悲観的な見通しをする人は100年以上前から何人もいて、そのたびに否定されてきています。
100年前の悲観論者が20世紀の数学の発展を見れば、自らの不明を恥じ入るでしょう。
しかし、こうした過去がありながら、数学で、あるいはもっと広く文明において「もうやることはないのではないか」といった問いかけが繰り返されています。
「研究し尽くされたのではないか?」という質問には、直接答えることができません。
この質問の答えは、各人の心の中にあり、各人がどのような知的な努力を行うかにかかっています。
数学の研究において知識の集積は必ずしも重要ではなく、創造的な人間の頭から生れるアイデアが重要になります。
それは過去の未解決問題を解くだけでなく、数学をより単純化しまた新しい研究の方向を照らし出すものです。
これによって、たえず数学の研究には長年蓄積された知識の資産がなくとも若くしてすぐれた成果をあげることが可能なのです。
また、数学の研究においては「知られた問題を解くこと」以上に「新たな問題を見出すこと」のほうが重要な意味を持つことが多いのです。
そして有名な未解決問題が解かれると、そこから新たな問題が生まれ新たな分野の発展を促すことも多いのです。
独創的な精神を人類が失う時代があれば、その時が数学の終わる時でしょう。「人間精神の名誉のために」(ヤコビの言葉)、若者が自由な思考を行う限り、数学の研究が尽きることは決してありません。
そして、数学者ほど知的な活動において完全な自由を持っている人間は少ないのです。
「もうやることはないのではないか?」という悲観論を抱く者に対しては、「あなたは自由な精神を本当の意味で持っているのか」という問いで答えたいと思います。
繰り返しますが、自由な精神が人間の名誉をかけてたゆまず思索する限り、いつまでも数学は前に進んで行くでしょう。
物理を学びたいと思い物理学科を志望している女子高生ですが、親にものすごく反対されています。
「物理学科で学んで、そのあとどうするの?」と親に聞かれると、言葉につまってしまいます。
私は宇宙などが好きで、もっと知りたいって思っているだけだからです。
親は阪大理学部を志望校にすることさえ許してくれません。どうすればいいですか?
「物理学専攻の男性の教授からの回答」
ご両親はあなたの将来を心配してご意見を言っているのであって、あなたを苦しめようと思っているわけではないことを、まずは忘れないようにしてください。また「宇宙などが好きで、もっと知りたいって思っているだけ」なのは、理学にとってはきわめて健全な動機です。理学の進歩は、設定された最終的具体的目標に向かって活動することによるのではなくその都度心に生じる自然な感情(好奇心)に駆動されているからです。
「物理学専攻の女性の教授からの回答」
まず、理系の学部には女子学生が少ない、というのは事実です。阪大理学部の物理で言えば、およそ全学生数の1割程度です。化学や生物では、もう少し女子学生の割合は多いと思います。理学部や工学部の学生は、卒業すると男女を問わず8割程度が大学院に進学します。博士前期課程(修士課程)2年間を終えると、2割くらいが博士後期課程(3年間)に進学し、残りは企業などに就職します。この段階で、女性だからといって就職率が悪いということは全くありません。今は男女雇用機会均等法がありますし、大企業は皆女性技術者(研究者)を男性と等しく扱ってくれます。もちろん、結婚や出産を機に退職する女性も多いですが、子供を育てながら研究や仕事を続けている女性も大勢います。また大学院を修了した後、国立研究所や大学の研究職につく人もある程度の割合おります。すぐに常勤ポストにつけない場合、非常勤の研究職を何年か勤める人も少なくありません。物理で博士号を取得した人達の就職率の低さは、確かに社会問題になっている、といってもいいかもしれませんが、これは本人がどれくらい柔軟に社会に対応できるかという問題であり、決して本当の意味で就職できないわけではないのです。
まだ、高校生のあなたには、学部4年間プラス大学院5年間の後の生活など、今想像できないでしょうからこの話はここでやめます。もし、大学4年間の後に企業に就職しようと思うのであれば、物理だろうが文学部だろうが、同じです。就職率が高いか否かは、その時の世の中の景気次第ですが、物理だから低いということは決してありません。むしろ理系のほうが、「手に職がある」という意味で有利だと思います。大学院卒業者についても同じです。女性であるから就職できない、などということは決してありません。もし一生研究を続けたいと希望される場合は、少し状況が違います。大学の教員ポストを得るのは、男性でもかなりの狭き門だからです。ここで女性が不利になることがないかと言われれば、正直に「現実は多分目に見えない壁がある」と言わざるをえません。でもこのような問題も少しずつ解決されていて、今は「女性だとむしろ有利だ」という世の中になってきている、と思います。そもそも、大学で勉強するのは何のためなのか、ということをよく考えてください。大学は就職するための職業訓練所ではありません。また就職のときに役立つ「ブランド」を手に入れるために大学に入るわけでもありません。知の欲求を満たすための学問をするところが、大学ではないでしょうか。それならば、卒業した後の人生設計ができていなくても構わないではありませんか。むしろ卒業後の人生設計が高校生で既にできている方がおかしい、くらいです。あなたが真剣に物理を勉強したい、と思うなら、ご両親にその思いを伝えてみたらいかがでしょう。学校の物理の先生にお願いして、ご両親を説得してもらうのも一つの手かもしれません。もう一度、答えを申し上げます。阪大理学部の卒業生は就職に困るようなことはありません。
女子学生だからといって就職できないこともありません。大学卒業後の進路については男女を問わず企業に就職する人の割合のほうが多いですが、大学などに残って研究職につく人も多いのは理学部の特色かもしれません。
理学部は就職に関して工学部より劣るのでしょうか?劣るとしたらどのぐらい劣るのでしょうか?
そして大体何パーセントの人が学部と修士あわせて就職できるのでしょうか?
資料などをみるとほとんどの人が修士までとっていて、その就職した企業の一覧とかはでているのですが何パーセントの人がちゃんと就職できているのかわからないのです。
あと博士課程までとってから研究職につける人はどれぐらいいるのですか?聞いたところによるとあまり研究職につける人はいないようなのです。
就いても給料がとても安く、苦労するというらしいと聞きました。
あくまで阪大に関してでかまいませんので教えてください。(高校3年生)
高校3年生と言うことで、将来の選択を色々と思案していることと思います。
就職状況についてですが、求人は非常に多く、ご心配されるような就職難はありません。比率としては、理学部の卒業生の2割程度が企業や高等学校教諭などに就職し残りの8割程度が大学院の博士前期課程(修士課程)に進学、大学院の博士前期課程(修士課程)修了者の7割程度が企業や高等学校教諭や国家公務員などに就職し、2割程度が大学院の博士後期課程に進学しています。博士後期課程で博士(理学)の学位を取得した方は、大学教員や研究所の研究員や企業の研究開発スタッフとして活躍しています。
企業への就職ですが、理学部・理学研究科に特徴的なこととして特定の業種に限定せず、様々な業種に広がっています。
大阪大学理学部および理学研究科では、数学・物理学・化学・生物科学の幅広い知識はもちろんのこと、複雑な自然現象を司る原理・原則、さらにそれを基盤とした論理的思考についてしっかりと学んだ上で、世界の最先端の研究を行っています。
企業でも新しい技術や製品の開発をする際には、複雑な事象の中から本質的な問題を抽出し解決する能力が求められます。そのような理由で、幅広い素養をもつ理学部/理学研究科の卒業生は貴重な人材として多方面から期待されており、毎年たくさんの求人が全国の企業や国の機関、高等学校などから届き、巣立って行きます。
僕はこの五年間ほどから宇宙論に強く興味を持っており当然ずっと理学部志望でいました。
しかし、実利がほとんど期待できないこの分野では研究をして生計を立てていけるのは、才能の面でも金銭の面でも限られた一握りの人だけで現実はそれほど甘くはないんだと徐々に気づきました。
それに就職を目指したところで、宇宙論にそれほど潰しが利くとは思えません。
それに矛盾した話かもしれないですが、僕には漠然と、「自分で、企業などにとっての実利となるなんらかの『財』的なモノを生み出したい」、「社会にできるだけ直接的に影響し、社会に必要とされていたい」といった憧れのようなものがあります。この希望は自分の興味のある分野の性質と相対することのように自分でも感じるのです。
「ポスドクまで行ったあげく、30歳で挫折してフリーター完成」のような事態は何としてでも避けたいし、周りの人たちの進めもあって工学部への転向を考えています。
しかし工学部という学部は、特定分野の就職に強い反面、大学に入る時点である程度自分の将来専攻すべき分野を決めておくことが求められると僕は聞いています。
あと一年でそれを決めるには、僕には時間と情報が少なすぎます。
苦しんでおりますが一年以内に最初の決定をしなければなりません。
なるべく将来に選択肢が残るような進路を教えていただけるようお願いします。
真剣に将来のことを考えておられる様子、大変感心致しました。
また色々とやりたいことを持っておられることは、将来それがどのような形でご自分に関わってくるのかによらず宝物です。
大切になさって下さい。
工学部や工学研究科等では企業などで応用に役立つ知識を学ぶことができます。
もし、具体的に希望するものがはっきりしているようでしたら、それを選択するのも良いと思います。
しかし、それで人生が決まると考えるのは、早すぎます。世の中には色々な仕事があります。また一生同じ仕事をしてゆくとは限りません。
ひとつの専門に限定されない広い知識も必要です。そのためには、常に研鑽を積むことを怠らないようにすることが大切です。
一方、理学部や理学研究科では基礎的な学問の研究を行っています。
物理系では、物理現象の基本を理解し解明してゆきます。
実験したり、計算したり、新しい理論を考案したりする中で、それまでわからなかったものが見えてきます。
その成果を世界中に発信します。仮に企業等に就職することを考えた場合でも、それらは十分に生かされます。
実際、大阪大学理学部物理学科およびその上にある大学院(物理学専攻と宇宙地球科学専攻)には沢山の求人が来ます。
卒業生は、工学部や工学研究科出身の人たちと共に活躍しています。
強いて言えば、工学系出身の人はその技術的な可能性を経験の中から突き詰めて技術開発や生産を行うのに対して、理学系出身の人は基本から理解して原理に基づく新しい技術の開発や生産を目指そうとします。実際はその両方が必要です。
また最近の傾向としては、IT関係の求人が増えています。高校教諭になる方もおられます。博士課程(博士後期課程)に進んだ場合でも、修士課程(博士前期課程)や学部生と応募方法に違いはありますが、民間企業に就職する方が増えています。物理学専攻のホームページには、卒業後の進路が掲載されていますのでご覧下さい。
もし研究に強い関心があり、しかもその能力があれば大学等のアカデミックな職につくことは十分可能です。
理学系の研究は必ずしも直接世の中の役に立つことを目指して研究しているわけではありませんが、その研究成果は人類の英知を育む知識の一端を担っています。
宇宙がどうやってできたのか、とか素粒子の根元を解明することは確かに我々の日常生活に直接変化はありません。
しかしそれを知ることによって、人類はより豊かな世界観をもつことができます。
なお、ポスドクという身分は、研究者が独り立ちするための期間と理解して下さい。
研究職に就くと、自分で研究テーマを提案し推進します。ポスドクなどの経験を経ることによって、新しい研究領域を開拓してゆく能力と次の世代を育ててゆく能力が更に身に付きます。
もちろん、物理学には宇宙論に限らず色々な学問があります。興味があったら是非入学を志して下さい。
たとえば、固体結晶が示す性質や機能の探求はそれ自体に尽くせない興味があるだけでなく、その基本原理は応用のための指針としても重要です。
また理学部では物理以外にも様々な基礎学問を研究している研究室があります。宇宙論でなければ工学部という発想はあてはまらないと思います。
ところで、何かひとつの仕事を成し遂げられる能力を持ったひとは他の仕事でもその能力は発揮できるものです。
現時点では、将来の選択肢について情報が十分ではないかも知れませんが、逆に「今、何かを選択したら将来が決まり、安泰」と期待するのも安易な考え方だと思いませんか。
大切なことは何事にも真剣に向かっていることです。
いつかチャンスがやってきたときにそれをものにします。いつも成長していること、それが大切です。
ちなみに「未熟」とは熟す過程にあることを意味します。それには上限はありません。年をとっても上を目指す「未熟者」でいたいものです。
ご健闘を祈ります。
就職者53名(民間就職50名、公務員3名)
これが理学部の修士課程終了した人の就職実績ですが、はっきりいってかなり悪いと思います。
確かに大学というのは就職するための予備校ではなく、勉強をするというところですから就職だけにこだわって考えるのはよくないことかもしれません。
しかし就職活動という言葉が存在しますし、大学を出たら自分で働いてお金を稼がなければならないので 、必然的に就職ということは重要視されるのは当たり前だと思います。
理学部の場合、中学高校の教師になる人が結構いますがそれは大学で勉強したことは全然いかされないでしょう。
生かすとしたらならどこかの企業の研究所に入るか、博士まで行って教授になって大学で研究するかのどちらかだと思います。
ただ企業の研究所に入って研究させてもらえるのも大学の教授になれるのも一握りの人です。また、
企業の研究所にも研究する範囲があるので素粒子などはまったく企業から相手にされません。
ポスドクもアカポスもものすごい倍率で落ちる人がかなりの人のはずです。ましてやノーベル賞なんて夢のまた夢です。
理学部物理学科に行って素粒子の研究職につくのがこんなに実現不可能に近いとは思ってませんでした。
理学部に行く目的がわからなくなりました。就職も他の学部に比べてきつい。研究者にもなるのが難しい。しかも素粒子なんかは教授以外に道が無い。
理学部に行く目的ってなんですか?教えてください。(高校生)
就職が「良い」「悪い」という場合に、様々な基準があると思われます。
どのような基準に照らして「悪い」とおっしゃられているのか不明ですが、一般的見地からは、本研究科の就職実績は全国的水準をはるかに上回っているものと考えられます。
しかし、「良い就職とは何か」といった問題は、1元的な価値基準で定まるものではないので就職実績だけから判断するのは大きな誤りです。
人生は長く高校時代に考えることとは全く別のことに興味を見いだし、大学・大学院で専攻を変えたり就職時さらには就職後にも職種を変えることはごくごく一般的です。
もしかすると貴君は10年後には素粒子物理学とは全く異なる分野の仕事をされているかも知れません。
しかし、もしも素粒子物理学研究よりも、よりあなたの適性に沿う専門領域があるとしたらそれを見いだしてもらうこと、それこそが大学・大学院教育の主目的なのです。
個人的経験に照らしても周囲の人々の話を総合しても、高校時代に考えることは極めて限定された知識のもとでの狭い狭い将来像でしかないことが多いです。
私も高校時代は物理学には素粒子理論と宇宙論しかないと思っていましたが、それは全くの誤りでした。物理学はもっともっと巨大な学問です。
物理学に興味をお持ちなら、是非大阪大学理学部物理学科に入学して、その広大な研究の地平を見渡す冒険に参加してみてください。
細かい個々の専門分野のおもしろさは講義やゼミを通じてお教えします。研究者の道を選ぶかどうか、企業に就職するか大学で研究するかどうかなどは、そのような冒険をしていく中で意志が固まっていくことでしょう。
そして大阪大学は、そのような適切な進路指導を行うことができる体制が整えられています。
大学院から別の研究科、場合によっては別の大学の大学院に進学することも推奨されています。
あらゆる専門領域のトップレベルの研究者・教授の「品揃え」により、適切な進路指導が可能であることが、総合研究大学院大学たる大阪大学の強みです。
高校生の段階から、いろいろな情報を集め、分析し、ここにも投稿されるというあなたの行動力には本当に感心させられます。
是非とも大阪大学に来て欲しいと思います。しかし、あまり高校生の段階から、その時の状況・情報だけから判断して将来について狭く考えることをしないでください。
ダイナミックに進路を切り開いていくこと、それがこれからの若い人々に期待される人生像ですし、それが可能になったのは日本でも本当に最近のことです。
それは新たに獲得された権利なのです。是非存分に行使していって頂きたいと思います。
このような多様な価値観が渦巻く社会の中で、理学部とその出身者が果たすことのできる役割とは何かを考えてみますと物事を根本的・抽象的・大局的な観点から系統的に捉えることにより問題の解決を行う、ということが挙げられると思われます。
具体的な理学の知識が直接問題の解決につながることはもちろんのこと、それ以上により広い範囲の理学を越えたあらゆる分野において、理学的な発想・視点が重要な役割を果たす場合が少なくないのです。
理学部出身で現在理学に直接関わる職種についていない人でも、そのような方々のお話でよく聞くのは「理学部出身でよかった」ということです。
前の教育審議会の主要メンバーである某小説家は、「私の人生において方程式など何の役にも立たなかった。方程式など知らなくても生きてこれた」といった趣旨の発言をされていましたが、これは教育に関わる公人の発言としては全く見識に欠けるものと言わざるを得ません。
むしろ常に世界のどこかで続いている戦争・紛争、もしくは、カルト宗教や、インチキ商法などの跳梁跋扈を見てもわかるように、政府、市民の合理的な判断力が大幅に低下している昨今にあっては理学的な発想を持つことは、今後人類が合理的に振る舞うための最後の砦と言っても過言ではないでしょう。
「方程式が人生に役に立たない」という発言は、物事を根本的につきつめて考えるという姿勢に対する、有史以来の「人間が陥りやすい安易なイデオロギー」からの攻撃を象徴しています。
ガリレオの宗教裁判の話はご存知かと思いますが、理学はずっとずっとそのような闘いを勝ち抜いてきました。
その強さが、その発想・思想・方法の正当性を雄弁に物語っています。もしも貴君が小中高校の夏休みの自由研究などを通じて、「何かに興味を持って、調べて、新しいことを発見する」ことにすでに喜びを見いだした経験があり「研究っておもしろそうだなぁ」と思っておられるならば、研究者として最も大切な適性の大半をすでに持っていることになります。
最近の風潮では、すぐにビジネスに結びつく近視眼的な応用研究のみがもてはやされて理学部に対する不当な風当たりも強いのですが、理学に興味をもたれた貴君のような貴重な同志には是非この長い長い研究の歴史に新たなものを付け加えていく活動に参入して欲しいと願っています。
最後に、上記の小説家の発言に対しては、同じ小説家である村上春樹氏の「ノルウェイの森」の中の一節を引用して答えとしたいと思います。
おそらく村上氏は理学の専門教育を受けたことはないかと思われますが、理学的視点・発想の重要性を直感的に理解されているのだと思います。
「ねぇワタナベ君、英語の仮定法現在と仮定法過去の違いをきちんと説明できる?」 と突然僕に質問した。
「できると思うよ」
と僕は言った。
「ちょっと訊きたいんだけれど、そういうのが日常生活の中で何かの役に立ってる?」
「日常生活の中で何かの役に立つということはあまりないね」
と僕は言った。
「でも具体的に何かの役に立つというよりは、 そういうのは物事をより系統的に捉えるための訓練になるんだと僕は思ってるけれど」
貴君の今後のご健闘とご発展をお祈りします。
僕は将来、理科の中学校の教員になろうと決めています。この気持ちは人一倍強いと自負しています。
僕が思うに、教員に求められるものは、教員になるまでにどれだけどんな経験を積み、教える教科を誰よりも深く知り、何より生徒を愛することだと思っています。
そこで、非常に興味のある貴校の理学部や工学部で学問や研究に没頭するか、教員養成系の学部に進学するか悩んでいます。
また中学校の教員になると決めている以上、教員養成系に進むのが教員になるための近道であり適しているのではないか、とも悩んでいます。
さらに、理学部に進むのならまだしも、工学部に進んでも大丈夫かな・・・、なんてわけのわからないことを考えたりもしています。
これらの悩みに対する「完璧な答え」はないと思われますが、何か手がかりが欲しいと切望しています。できるだけ詳しい回答をお願いします。
(生物科学専攻の先生から)
小学校の教員免許は全教科担当になるので、教員養成学部(教育大学や学芸大学)に入学しないと実質的に取得不可能ですが、中学・高校の教員免許は専科担当になるので、理学部に在籍していても取得できます。現実に理学部のかなりの数の学生諸君が在学中に免許をとります(数学科の諸君は数学の、物理・化学・生物科学科の諸君は理科の教員免許がとれます)。ただし、理学部の講義をとる以外にいくつかの教職科目を余計にとらなくてはならないので、忙しいのは事実ですが。
回答者の私見になりますが、中学・高校の先生でも教職のために理科の教育方法を教わった「教育のプロ」の先生より、自分の専門研究分野を持っている(あるいは専門の研究の経験がある)先生の方が、魅力的なように思います。
少なくとも私が中学生・高校生のときは、そう思いました。ある理科の先生は学生時代理学部で地質学を専攻しておられたのですが、授業が終わると理科室の隣の理科準備室をご自分で改造した研究室にこもって、熱心に化石を割り出していました。私が何かの用事でそこを訪ねていくと、理科の授業中とは全く違った顔で楽しそうにご自分の研究を話してくださる、それを聴きながら私もよくわからないけれど一緒に興奮し、最初の用事が何だったか忘れてしまう。
そんな経験が、今私が研究者をやっている原因の一つになっているような気がします。
(事務部学務係から)
大阪大学理学部を卒業して中学校教諭一種免許状を取得するためには、教育実習等を含めた「教育の基礎的理解に関する科目等」合計27単位、特別支援学校、社会福祉施設等で実施する7日以上の「介護等の体験」(実習)を卒業要件単位とは別に修得する必要があります。
教員養成系の大学との大きな違いは、【卒業要件単位とは別に】単位を修得する必要があることだと思います。
なお、大阪大学では、工学部、基礎工学部、理学部で中学校教諭一種免許状(理科)を取得することが可能です。
URL:取得できる取得できる免許状の一覧
現在地元の小学校に通う2年生の娘が〔お医者さんになりたい〕と言い続けています。
最初はこちらも〔ふーん〕と軽く聞き流していたのですが最近〔どうすればお医者さんになれるのか〕と質問されます。〔うんと勉強してがんばってなるんやで〕と言っても〔どんな勉強?どんなことしたらええん?〕と詳しく聞いてくるので返答に行き詰まり困っています。
小2が理解しやすい説明を教えて頂きたいのですが、よろしくお願いします。
小学生の段階で医師になるための勉強というのはありません。私は医師ではありませんが、たくさんの医師の知人をもっていえることは、三つあります。
一つ目。医学は自然科学です。おまじないではないので、自然科学者としての目を育ててほしいと思います。
小学生にわかるようないい方をすれば「理科大好き」になってほしいということです。それには、本でお勉強するのはほどほどにして、それ以上に自然に触れたくさんの不思議を体験してください。春夏秋冬季節が巡るのを不思議に思い、星を見てどうして光るのか不思議に思い、卵からオタマジャクシが出てきてやがてカエルになるのを不思議に思うことです。
ご両親としては、その不思議に本で読んですぐに解答を与えてしまうのではなく、いっしょに考えてやってください。
正解は出なくてもかまわない、不思議のままでもかまわないのです。自分で考えて答えを見つける喜び(たとえ本当はそれが間違いであっても)こそ自然科学の原動力ですから。
二つ目。医療は一種の接客業です。病気と向き合うだけでなく、患者さんと向き合って患者さんの苦しみを分かってあげることが出発点です。
ですからお勉強部屋に閉じこもって成績を上げるより、たくさんの人と出会っていろんなお友達をもち、「こういう人もいるんだ」「こういう考えをする人もいるんだ」という体験を積んでほしいと思います。
三つ目。医術は重労働です。外科医は6時間くらい立ちっぱなしで神経を張り詰めて作業することは珍しくありません。内科医は自分の体調が悪かろうと疲れていようと、急患の連絡を受ければ往診に出向かなければなりません。
ですから、体力が基本です。「スポーツ大好き」、できたらアウトドアスポーツ大好きになってください。
ということは結局、外で自然に触れながら友達と元気に遊んでください、ということに尽きます。
阪大を受けることになれば、通学におよそ2時間かかることが分かり下宿をするかどうか迷っています。
他の生徒の平均通学時間と下宿する関係が知りたいです。
これについての正式なデータがあるのかどうか、ちょっと分かりません。
しかし、 奈良や姫路、和歌山や京都の北の方からも通っている人が少なからずいることは事実です。学生実験や実際の研究生活が始まると、実験が終わる時間はマチマチで、予想以上に遅くまでかかることもありますので、下宿が近くにあると安心だとは思います。
理学部では大学院に進学する人が多いようですがどうしてでしょうか。
確かにかなり多いといえるでしょう。これには主に2つの理由が考えられます。まず、一般的に理学部の学生はもともと学究心・研究心に富む人が多く、学部での学究的雰囲気の中で研究を始めるようになると、教科書には書かれていない「最先端科学」に興味を覚え、大学院に進学してさらに深く学び、経験を積み、さらには自分も「知」を創出したいと希望するようになります。次はもっと現実的ですが、企業の研究部門では、研究経験を積んだ修士や博士の人を求める傾向にあり、それを考慮して進学する人もいます。いずれにしても、多くの人が大学院生の間に研究者として大きな成長を遂げます。
資格取得について
僕は高校2年生で将来中学校の数学の教師になろうと考えています。
教員養成学部以外での免許の取得が難しくなったそうですが、理学部の数学科からでは教師になるのは大変になるのでしょうか?
いろいろ進路の事で真面目に悩んでいるのでよろしくお願いします。
大阪大学理学部数学科では、卒業時に中学校教諭一種免許状(数学)や高等学校教諭一種免許状(数学)を取得することができます。ただし、数学科に配当されている一般教養科目・専門教育科目の他に、「教育の基礎的理解に関する科目等」と呼ばれる科目を、理学部数学科の卒業要件単位とは別に27単位修得する必要があります。この中に中学校や高校で実施する「教育実習」も含まれます(学部4年次に実施)。また、中学校教諭一種免許状を取得する際は、社会福祉施設や特別支援学校での「介護等の体験」が必要になります(主に学部3年次に実施)。
大阪大学理学部数学科の少なくとも1/3位の学生は卒業までに教員免許を取得しています。ですから、教員免許を取得することがそれほど大変と言うわけではありません。
また、教員免許を取得するのであれば、大阪大学在学中に、中学、高校両方の教員免許を取得することを薦めています。(理学部では多くの学生が頑張って両方取得するようにしています。)
大阪大学数学科では、教員養成大学よりはるかに視野の広いバランスのとれた教育を行っているという自負があります。ティーチングスタッフも研究の最前線で活躍している人がほとんどで充実しています。
在学時、教職課程の単位を取りましたが、教育実習をせずに免状はとりませんでした。理学部卒業、工学研究科修了に高校理科の教員の免状を取得できるでしょうか?
大阪大学の科目等履修生として「教育実習」を修得することができます。
ただし教育実習を履修するために事前に修得しておかなければならない科目が多数あり、 それらをすべて修得していることが条件です。
また、教育実習を履修する年の前年に 大阪大学から実習校宛に「教育実習受け入れ内諾依頼」を行い、 その年の内に実習校から内諾を受けておく必要があります。
その上で、科目等履修生に出願しなければなりません。
詳しくは、大阪大学理学部学務係までお問い合わせください。
大学院に入学後、教育実習など教員免許を取得するのに必要な科目を、学部に受講しに行くことはできるのでしょうか。
現在、他大学に在籍していて大阪大学大学院への進学を考えています。今教職課程をとっているのですが学部中に全ての単位を修得できそうにありません。
大学院に入学後、教育実習など教員免許を取得するのに必要な科目を学部に受講しに行くことはできるのでしょうか。(大学3年生)
大阪大学理学部・大学院理学研究科では、数学・理科の科目について、中学校教諭一種・ 専修、高等学校教諭一種・専修の免許状を申請するための単位を修得することができます。
大学院に入学後、学部科目を受講し修得することは可能です。
僕は朝鮮大学校の理工学部で物理を専攻しています。
卒業後、大阪大学大学院理学研究科・博士前期過程の入試を受けようと思ってるんですが、現在の時点で朝鮮大学校は各種学校として認定されています。
朝鮮大学校の卒業生が受験資格を得るには特別な審査が必要になってくるのでしょうか?
それとも、一般の大学の卒業生と同じように受験資格が与えられるのでしょうか?
個別の入学資格審査を受けていただき、審査の結果、大学を卒業した者と同等以上の学力があると認められ、入学を希望する年の3月31日で満22歳に達している方が出願できます(4月入学の場合)。
詳細については、お手数ですが大阪大学理学研究科大学院係までお問い合わせください。
大阪大学理学部物理学科の三回生ですが、今から数学の教員免許を取ることは可能でしょうか?
大学院には進もうと思っているので、大学院を卒業するまでに取ったりすることは可能でしょうか?
厳しいならば、どれぐらい厳しいかも具体的に教えていただきたいです。
大阪大学理学部では、中学校教諭、高等学校教諭の一種免許「数学」「理科」を、大学院理学研究科では中学校教諭、高等学校教諭の専修免許「数学」「理科」に必要な単位を修得することができます。大学院に入学後、学部科目を受講し単位を修得することも可能です。
物理学科および大学院(物理学専攻・宇宙地球科学専攻)在籍中に、数学科で開講される「教科に関する専門的事項」「大学が独自に設定する科目」及び「数学科教育法」の単位を修得することで、数学の免許状を取得することができます。
ただし物理学科および大学院(物理学専攻・宇宙地球科学専攻)での本来の勉強がありますので、その合間をぬって教職の単位を修得しなくてはなりません。加えて、理科の免許状を取得する場合よりも多くの単位を修得する必要があります。
また数学科と授業の時間帯が被り、卒業・修了するまでに数学の教職に必要な単位を修得しきれない可能性もあります。そのため学部の時になるべく多くの単位を修得しておくことをお勧めします。
さらに、「教科に関する専門的事項」( 20単位)はあくまで免許状取得の最低ラインであり、実際に教壇に立つには「教科に関する専門的事項」となっていない専門教育科目等も含めた深い専門分野の知識が求められます。
そうした他の学科の専門分野についても自ら学習しなければなりませんので、綿密に学習計画を立てて履修を進める必要があります。












